| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 8 Introduction To Trigonometry
Welcome to the solutions for Chapter 8: Introduction to Trigonometry. This chapter opens the door to a fascinating and essential branch of mathematics that deals specifically with the relationships between the angles and the side lengths of triangles. The term "trigonometry" itself originates from Greek words meaning "triangle measurement." While trigonometry has vast applications in fields like physics, engineering, navigation, astronomy, and even music theory, this introductory chapter focuses squarely on the foundational concepts derived from right-angled triangles. We will explore how the ratios of the sides of a right triangle are uniquely determined by its acute angles, leading to the definition of the fundamental trigonometric ratios. These ratios provide a powerful way to link angles and lengths, enabling us to calculate unknown sides or angles when partial information is available. Mastering these initial concepts is crucial for further study in mathematics and science.
The cornerstone of this chapter is the definition of the six trigonometric ratios for an acute angle, let's call it $\theta$, within a right-angled triangle. These ratios relate the angle $\theta$ to the lengths of the triangle's sides: the side opposite to $\theta$ (Perpendicular, $P$), the side adjacent to $\theta$ (Base, $B$), and the side opposite the right angle (Hypotenuse, $H$). It's vital to remember that the identification of 'Perpendicular' and 'Base' is always relative to the acute angle $\theta$ being considered. The six ratios are defined as follows:
- Sine: $\sin \theta = \frac{\text{Perpendicular}}{\text{Hypotenuse}} = \frac{P}{H}$
- Cosine: $\cos \theta = \frac{\text{Base}}{\text{Hypotenuse}} = \frac{B}{H}$
- Tangent: $\tan \theta = \frac{\text{Perpendicular}}{\text{Base}} = \frac{P}{B}$
- Cosecant (reciprocal of sine): $\text{cosec } \theta = \frac{\text{Hypotenuse}}{\text{Perpendicular}} = \frac{H}{P}$
- Secant (reciprocal of cosine): $\sec \theta = \frac{\text{Hypotenuse}}{\text{Base}} = \frac{H}{B}$
- Cotangent (reciprocal of tangent): $\cot \theta = \frac{\text{Base}}{\text{Perpendicular}} = \frac{B}{P}$
Solutions demonstrate how to calculate these ratios when the side lengths are known. Conversely, if one trigonometric ratio is given, we can often find the lengths of the sides (or their proportions) using the definition and the Pythagorean theorem ($P^2 + B^2 = H^2$), subsequently allowing the calculation of the other five ratios.
A significant part of the chapter involves evaluating trigonometric ratios for specific standard angles: $0^\circ, 30^\circ, 45^\circ, 60^\circ,$ and $90^\circ$. The solutions often show how these values are derived geometrically (using equilateral and isosceles right triangles) and present them in a table for easy reference. Extensive practice is provided in substituting these standard values into various trigonometric expressions and evaluating them. Furthermore, the inherent relationships between the ratios are highlighted and utilized, such as the quotient identity $\tan \theta = \frac{\sin \theta}{\cos \theta}$ and the reciprocal identities like $\text{cosec } \theta = \frac{1}{\sin \theta}$.
The concept of complementary angles (two angles summing to $90^\circ$) leads to another set of important identities. Since the two acute angles in a right triangle are complementary, relationships emerge such as $\sin(90^\circ - \theta) = \cos \theta$, $\cos(90^\circ - \theta) = \sin \theta$, and $\tan(90^\circ - \theta) = \cot \theta$, along with corresponding identities for the reciprocal functions. The solutions demonstrate how applying these trigonometric ratios of complementary angles can simplify expressions involving angles like $18^\circ$ and $72^\circ$, or $25^\circ$ and $65^\circ$.
Finally, the chapter culminates in the introduction and proof of the three fundamental Pythagorean trigonometric identities, which are true for any angle $\theta$:
- $\sin^2\theta + \cos^2\theta = 1$
- $1 + \tan^2\theta = \sec^2\theta$
- $1 + \cot^2\theta = \text{cosec}^2\theta$
These identities are immensely important in trigonometry. The solutions extensively demonstrate their application in proving other, more complex trigonometric relationships (proving LHS = RHS) and in simplifying intricate trigonometric expressions. This chapter lays the essential groundwork for all future work involving trigonometry.
Example 1 to 5 (Before Exercise 8.1)
Example 1. Given tan A = $\frac{4}{3}$ , find the other trigonometric ratios of the angle A.
Answer:
Given:
$\tan A = \frac{4}{3}$
To Find:
The other trigonometric ratios of the angle A.
Solution:
Consider a right-angled triangle ABC, right-angled at B, with respect to angle A.
In a right triangle, the trigonometric ratio $\tan A$ is defined as the ratio of the side opposite to angle A to the side adjacent to angle A.
$\tan A = \frac{\text{Side opposite to angle A}}{\text{Side adjacent to angle A}} = \frac{BC}{AB}$
We are given $\tan A = \frac{4}{3}$.
So, $\frac{BC}{AB} = \frac{4}{3}$.
Let $BC = 4k$ and $AB = 3k$, where $k$ is a positive constant.
By the Pythagorean theorem in $\triangle$ ABC:
$AC^2 = AB^2 + BC^2$
$AC^2 = (3k)^2 + (4k)^2$
$AC^2 = 9k^2 + 16k^2$
$AC^2 = 25k^2$
$AC = \sqrt{25k^2} = 5k$ (Since length is positive)
Now we can find the other trigonometric ratios:
$\sin A = \frac{\text{Side opposite to angle A}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{4k}{5k} = \frac{4}{5}$
$\cos A = \frac{\text{Side adjacent to angle A}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{3k}{5k} = \frac{3}{5}$
$\text{cosec } A = \frac{1}{\sin A} = \frac{\text{Hypotenuse}}{\text{Side opposite to angle A}} = \frac{AC}{BC} = \frac{5k}{4k} = \frac{5}{4}$
$\sec A = \frac{1}{\cos A} = \frac{\text{Hypotenuse}}{\text{Side adjacent to angle A}} = \frac{AC}{AB} = \frac{5k}{3k} = \frac{5}{3}$
$\cot A = \frac{1}{\tan A} = \frac{\text{Side adjacent to angle A}}{\text{Side opposite to angle A}} = \frac{AB}{BC} = \frac{3k}{4k} = \frac{3}{4}$
The other trigonometric ratios of angle A are:
$\sin A = \frac{4}{5}$
$\cos A = \frac{3}{5}$
$\text{cosec } A = \frac{5}{4}$
$\sec A = \frac{5}{3}$
$\cot A = \frac{3}{4}$
Example 2. If ∠B and ∠Q are acute angles such that sin B = sin Q, then prove that ∠B = ∠Q.
Answer:
Given:
$\angle$B and $\angle$Q are acute angles.
$\sin$ B = $\sin$ Q.
To Prove:
$\angle$B = $\angle$Q.
Solution:
Consider two right-angled triangles, $\triangle$ ABC and $\triangle$ PQR, where $\angle$C is right-angled in $\triangle$ ABC and $\angle$R is right-angled in $\triangle$ PQR. Let $\angle$B be in $\triangle$ ABC and $\angle$Q be in $\triangle$ PQR, and both $\angle$B and $\angle$Q are acute angles.
By the definition of the sine ratio:
In $\triangle$ ABC, $\sin$ B = $\frac{\text{Side opposite to }\angle\text{B}}{\text{Hypotenuse}} = \frac{AC}{AB}$
In $\triangle$ PQR, $\sin$ Q = $\frac{\text{Side opposite to }\angle\text{Q}}{\text{Hypotenuse}} = \frac{PR}{PQ}$
We are given that $\sin$ B = $\sin$ Q.
$\frac{AC}{AB} = \frac{PR}{PQ}$
…(i)
Let $\frac{AC}{AB} = \frac{PR}{PQ} = k$, where $k$ is a positive constant.
Then, $AC = k \cdot AB$ and $PR = k \cdot PQ$.
Using the Pythagorean theorem in $\triangle$ ABC:
$BC^2 = AB^2 - AC^2$
$BC = \sqrt{AB^2 - AC^2} = \sqrt{AB^2 - (k \cdot AB)^2} = \sqrt{AB^2 - k^2 AB^2} = \sqrt{AB^2(1 - k^2)} = AB \sqrt{1 - k^2}$
Using the Pythagorean theorem in $\triangle$ PQR:
$QR^2 = PQ^2 - PR^2$
$QR = \sqrt{PQ^2 - PR^2} = \sqrt{PQ^2 - (k \cdot PQ)^2} = \sqrt{PQ^2 - k^2 PQ^2} = \sqrt{PQ^2(1 - k^2)} = PQ \sqrt{1 - k^2}$
Now consider the ratio of the other pair of corresponding sides, BC and QR:
$\frac{BC}{QR} = \frac{AB \sqrt{1 - k^2}}{PQ \sqrt{1 - k^2}}$
Assuming $1 - k^2 \neq 0$ (which must be true for acute angles, as $k = \sin B = \sin Q$ and $\sin$ of an acute angle is between 0 and 1), we can cancel $\sqrt{1 - k^2}$.
$\frac{BC}{QR} = \frac{AB}{PQ}$
From equation (i), we have $\frac{AC}{PR} = \frac{AB}{PQ}$ (by rearranging the terms).
So, we have the ratios of corresponding sides equal:
$\frac{AC}{PR} = \frac{AB}{PQ} = \frac{BC}{QR}$
Since the ratios of all three pairs of corresponding sides are equal, $\triangle$ ABC is similar to $\triangle$ PQR by the SSS similarity criterion.
$\triangle$ ABC $\sim$ $\triangle$ PQR
(SSS similarity)
When two triangles are similar, their corresponding angles are equal.
Therefore, $\angle$B = $\angle$Q.
Hence Proved.
Example 3. Consider ∆ ACB, right-angled at C, in which AB = 29 units, BC = 21 units and ∠ABC = θ (see Fig. 8.10). Determine the values of
(i) cos2 θ + sin2 θ,
(ii) cos2 θ – sin2 θ.

Answer:
Given:
In $\triangle$ ACB, $\angle$C = $90^\circ$, AB = 29 units, BC = 21 units, and $\angle$ABC = $\theta$.
To Find:
(i) $\cos^2 \theta + \sin^2 \theta$
(ii) $\cos^2 \theta - \sin^2 \theta$
Solution:
In the right-angled $\triangle$ ACB, by the Pythagorean theorem, we have:
$AB^2 = AC^2 + BC^2$
$(29)^2 = AC^2 + (21)^2$
$841 = AC^2 + 441$
$AC^2 = 841 - 441$
$AC^2 = 400$
$AC = \sqrt{400} = 20$ units (Since length is positive)
Now, we determine the trigonometric ratios $\sin \theta$ and $\cos \theta$ with respect to angle $\theta$ ($\angle$ABC):
$\sin \theta = \frac{\text{Side opposite to }\theta}{\text{Hypotenuse}} = \frac{AC}{AB} = \frac{20}{29}$
$\cos \theta = \frac{\text{Side adjacent to }\theta}{\text{Hypotenuse}} = \frac{BC}{AB} = \frac{21}{29}$
(i) Value of $\cos^2 \theta + \sin^2 \theta$:
$\cos^2 \theta + \sin^2 \theta = \left(\frac{21}{29}\right)^2 + \left(\frac{20}{29}\right)^2$
$= \frac{21^2}{29^2} + \frac{20^2}{29^2}$
$= \frac{441}{841} + \frac{400}{841}$
$= \frac{441 + 400}{841}$
$= \frac{841}{841} = 1$
So, $\cos^2 \theta + \sin^2 \theta = 1$.
(ii) Value of $\cos^2 \theta - \sin^2 \theta$:
$\cos^2 \theta - \sin^2 \theta = \left(\frac{21}{29}\right)^2 - \left(\frac{20}{29}\right)^2$
$= \frac{21^2}{29^2} - \frac{20^2}{29^2}$
$= \frac{441}{841} - \frac{400}{841}$
$= \frac{441 - 400}{841}$
$= \frac{41}{841}$
So, $\cos^2 \theta - \sin^2 \theta = \frac{41}{841}$.
Example 4. In a right triangle ABC, right-angled at B, if tan A = 1, then verify that 2 sin A cos A = 1.
Answer:
Given:
In $\triangle$ ABC, $\angle$B = $90^\circ$ and $\tan A = 1$.
To Verify:
$2 \sin A \cos A = 1$.
Solution:
In a right triangle ABC, right-angled at B, the trigonometric ratio $\tan A$ is defined as the ratio of the side opposite to angle A to the side adjacent to angle A.
$\tan A = \frac{\text{Side opposite to angle A}}{\text{Side adjacent to angle A}} = \frac{BC}{AB}$
We are given $\tan A = 1$.
So, $\frac{BC}{AB} = 1$, which implies $BC = AB$.
Let $AB = BC = k$, where $k$ is a positive real number.
By the Pythagorean theorem in $\triangle$ ABC, the hypotenuse AC is:
$AC^2 = AB^2 + BC^2$
$AC^2 = k^2 + k^2$
$AC^2 = 2k^2$
$AC = \sqrt{2k^2} = k\sqrt{2}$ (Since length is positive)
Now, we find the values of $\sin A$ and $\cos A$:
$\sin A = \frac{\text{Side opposite to angle A}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{k}{k\sqrt{2}} = \frac{1}{\sqrt{2}}$
$\cos A = \frac{\text{Side adjacent to angle A}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{k}{k\sqrt{2}} = \frac{1}{\sqrt{2}}$
Now, we evaluate the expression $2 \sin A \cos A$:
$2 \sin A \cos A = 2 \times \left(\frac{1}{\sqrt{2}}\right) \times \left(\frac{1}{\sqrt{2}}\right)$
$= 2 \times \frac{1}{\sqrt{2} \times \sqrt{2}}$
$= 2 \times \frac{1}{2}$
$= \frac{2}{2} = 1$
$2 \sin A \cos A = 1$
Thus, we have verified that $2 \sin A \cos A = 1$ when $\tan A = 1$ in a right-angled triangle at B.
Alternate Solution:
We are given $\tan A = 1$.
We know that $\tan 45^\circ = 1$. Since A is an acute angle in a right triangle, this implies that $A = 45^\circ$.
Now, we find $\sin A$ and $\cos A$ for $A = 45^\circ$:
$\sin 45^\circ = \frac{1}{\sqrt{2}}$
$\cos 45^\circ = \frac{1}{\sqrt{2}}$
Substitute these values into the expression $2 \sin A \cos A$:
$2 \sin A \cos A = 2 \times \sin 45^\circ \times \cos 45^\circ$
$= 2 \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}$
$= 2 \times \frac{1}{2}$
$= 1$
Thus, $2 \sin A \cos A = 1$ is verified.
Example 5. In ∆ OPQ, right-angled at P, OP = 7 cm and OQ – PQ = 1 cm (see Fig. 8.12). Determine the values of sin Q and cos Q.
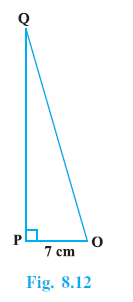
Answer:
Given:
In $\triangle$ OPQ, $\angle$P = $90^\circ$, OP = 7 cm and OQ – PQ = 1 cm.
To Find:
The values of $\sin$ Q and $\cos$ Q.
Solution:
In the right-angled $\triangle$ OPQ, we are given:
OP = 7 cm
OQ – PQ = 1 cm
... (i)
From equation (i), we can express OQ in terms of PQ:
OQ = PQ + 1
Applying the Pythagorean theorem to $\triangle$ OPQ:
$OQ^2 = OP^2 + PQ^2$
Substitute the values from the given information and the relation between OQ and PQ:
$(PQ + 1)^2 = (7)^2 + PQ^2$
Expand the left side using $(a+b)^2 = a^2 + 2ab + b^2$:
$PQ^2 + 2(PQ)(1) + 1^2 = 49 + PQ^2$
$PQ^2 + 2PQ + 1 = 49 + PQ^2$
Subtract $PQ^2$ from both sides:
$2PQ + 1 = 49$
Subtract 1 from both sides:
$2PQ = 49 - 1$
$2PQ = 48$
Divide by 2:
$PQ = \frac{48}{2}$
$PQ = 24$ cm
Now substitute the value of PQ into the relation OQ = PQ + 1:
$OQ = 24 + 1$
$OQ = 25$ cm
So, the lengths of the sides are OP = 7 cm (Opposite to angle Q), PQ = 24 cm (Adjacent to angle Q), and OQ = 25 cm (Hypotenuse).
Now, we can find the values of $\sin$ Q and $\cos$ Q:
$\sin Q = \frac{\text{Side opposite to angle Q}}{\text{Hypotenuse}} = \frac{OP}{OQ}$
$\sin Q = \frac{7}{25}$
$\cos Q = \frac{\text{Side adjacent to angle Q}}{\text{Hypotenuse}} = \frac{PQ}{OQ}$
$\cos Q = \frac{24}{25}$
The values are $\sin Q = \frac{7}{25}$ and $\cos Q = \frac{24}{25}$.
Exercise 8.1
Question 1. In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine :
(i) sin A, cos A
(ii) sin C, cos C
Answer:
Given:
In $\triangle$ ABC, $\angle$B = $90^\circ$, AB = 24 cm, BC = 7 cm.
To Find:
(i) $\sin$ A, $\cos$ A
(ii) $\sin$ C, $\cos$ C
Solution:
In the right-angled $\triangle$ ABC, by the Pythagorean theorem, we have:
$AC^2 = AB^2 + BC^2$
$AC^2 = (24)^2 + (7)^2$
$AC^2 = 576 + 49$
$AC^2 = 625$
$AC = \sqrt{625}$
$AC = 25$ cm (Since length must be positive)
(i) Values of $\sin$ A and $\cos$ A (with respect to angle A):
The side opposite to angle A is BC.
The side adjacent to angle A is AB.
The hypotenuse is AC.
$\sin A = \frac{\text{Side opposite to angle A}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{7}{25}$
$\cos A = \frac{\text{Side adjacent to angle A}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{24}{25}$
(ii) Values of $\sin$ C and $\cos$ C (with respect to angle C):
The side opposite to angle C is AB.
The side adjacent to angle C is BC.
The hypotenuse is AC.
$\sin C = \frac{\text{Side opposite to angle C}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{24}{25}$
$\cos C = \frac{\text{Side adjacent to angle C}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{7}{25}$
Question 2. In Fig. 8.13, find tan P – cot R.
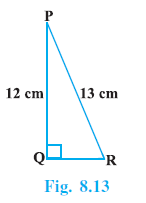
Answer:
Given:
In $\triangle$ PQR, $\angle$Q = $90^\circ$, PQ = 12 cm, PR = 13 cm.
To Find:
$\tan$ P – $\cot$ R.
Solution:
In the right-angled $\triangle$ PQR, by the Pythagorean theorem, we have:
$PR^2 = PQ^2 + QR^2$
$(13)^2 = (12)^2 + QR^2$
$169 = 144 + QR^2$
$QR^2 = 169 - 144$
$QR^2 = 25$
$QR = \sqrt{25}$
$QR = 5$ cm (Since length must be positive)
Now, we find the values of $\tan$ P and $\cot$ R.
For angle P:
The side opposite to angle P is QR.
The side adjacent to angle P is PQ.
$\tan P = \frac{\text{Side opposite to angle P}}{\text{Side adjacent to angle P}} = \frac{QR}{PQ} = \frac{5}{12}$
For angle R:
The side opposite to angle R is PQ.
The side adjacent to angle R is QR.
$\cot R = \frac{\text{Side adjacent to angle R}}{\text{Side opposite to angle R}} = \frac{QR}{PQ} = \frac{5}{12}$
Now, we calculate $\tan$ P – $\cot$ R:
$\tan P - \cot R = \frac{5}{12} - \frac{5}{12}$
$\tan P - \cot R = 0$
Question 3. If sin A = $\frac{3}{4}$ , calculate cos A and tan A.
Answer:
Given:
$\sin A = \frac{3}{4}$
To Find:
$\cos A$ and $\tan A$.
Solution:
We are given $\sin A = \frac{3}{4}$.
In a right-angled triangle, $\sin A$ is defined as the ratio of the side opposite to angle A to the hypotenuse.
Let's consider a right triangle ABC, right-angled at B, with respect to angle A.
$\sin A = \frac{\text{Side opposite to angle A}}{\text{Hypotenuse}} = \frac{BC}{AC}$
So, $\frac{BC}{AC} = \frac{3}{4}$.
Let $BC = 3k$ and $AC = 4k$, where $k$ is a positive constant.
By the Pythagorean theorem in $\triangle$ ABC:
$AC^2 = AB^2 + BC^2$
$(4k)^2 = AB^2 + (3k)^2$
$16k^2 = AB^2 + 9k^2$
$AB^2 = 16k^2 - 9k^2$
$AB^2 = 7k^2$
$AB = \sqrt{7k^2} = k\sqrt{7}$ (Since length is positive)
Now, we can find $\cos A$ and $\tan A$:
$\cos A = \frac{\text{Side adjacent to angle A}}{\text{Hypotenuse}} = \frac{AB}{AC}$
$\cos A = \frac{k\sqrt{7}}{4k} = \frac{\sqrt{7}}{4}$
$\tan A = \frac{\text{Side opposite to angle A}}{\text{Side adjacent to angle A}} = \frac{BC}{AB}$
$\tan A = \frac{3k}{k\sqrt{7}} = \frac{3}{\sqrt{7}}$
We can rationalize the denominator for $\tan A$:
$\tan A = \frac{3}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}} = \frac{3\sqrt{7}}{7}$
Thus, $\cos A = \frac{\sqrt{7}}{4}$ and $\tan A = \frac{3\sqrt{7}}{7}$ (or $\frac{3}{\sqrt{7}}$).
Question 4. Given 15 cot A = 8, find sin A and sec A.
Answer:
Given:
$15 \cot A = 8$
To Find:
$\sin A$ and $\sec A$.
Solution:
We are given the equation $15 \cot A = 8$.
Dividing both sides by 15, we get:
$\cot A = \frac{8}{15}$
In a right-angled triangle, the trigonometric ratio $\cot A$ is defined as the ratio of the side adjacent to angle A to the side opposite to angle A.
Let's consider a right triangle ABC, right-angled at B, with respect to angle A.
$\cot A = \frac{\text{Side adjacent to angle A}}{\text{Side opposite to angle A}} = \frac{AB}{BC}$
So, $\frac{AB}{BC} = \frac{8}{15}$.
Let $AB = 8k$ and $BC = 15k$, where $k$ is a positive constant.
By the Pythagorean theorem in $\triangle$ ABC:
$AC^2 = AB^2 + BC^2$
$AC^2 = (8k)^2 + (15k)^2$
$AC^2 = 64k^2 + 225k^2$
$AC^2 = 289k^2$
$AC = \sqrt{289k^2} = 17k$ (Since length must be positive)
Now, we can find $\sin A$ and $\sec A$:
$\sin A = \frac{\text{Side opposite to angle A}}{\text{Hypotenuse}} = \frac{BC}{AC}$
$\sin A = \frac{15k}{17k} = \frac{15}{17}$
$\sec A = \frac{\text{Hypotenuse}}{\text{Side adjacent to angle A}} = \frac{AC}{AB}$
$\sec A = \frac{17k}{8k} = \frac{17}{8}$
Thus, $\sin A = \frac{15}{17}$ and $\sec A = \frac{17}{8}$.
Question 5. Given sec θ = $\frac{13}{12}$, calculate all other trigonometric ratios.
Answer:
Given:
$\sec \theta = \frac{13}{12}$
To Find:
All other trigonometric ratios.
Solution:
We are given $\sec \theta = \frac{13}{12}$.
In a right-angled triangle, the trigonometric ratio $\sec \theta$ is defined as the ratio of the hypotenuse to the side adjacent to angle $\theta$.
Let's consider a right triangle ABC, right-angled at B, with respect to angle $\theta$ at A.
$\sec \theta = \frac{\text{Hypotenuse}}{\text{Side adjacent to angle }\theta} = \frac{AC}{AB}$
So, $\frac{AC}{AB} = \frac{13}{12}$.
Let $AC = 13k$ and $AB = 12k$, where $k$ is a positive constant.
By the Pythagorean theorem in $\triangle$ ABC:
$AC^2 = AB^2 + BC^2$
$(13k)^2 = (12k)^2 + BC^2$
$169k^2 = 144k^2 + BC^2$
$BC^2 = 169k^2 - 144k^2$
$BC^2 = 25k^2$
$BC = \sqrt{25k^2} = 5k$ (Since length must be positive)
Now, we can find the other trigonometric ratios:
$\sin \theta = \frac{\text{Side opposite to angle }\theta}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{5k}{13k} = \frac{5}{13}$
$\cos \theta = \frac{\text{Side adjacent to angle }\theta}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{12k}{13k} = \frac{12}{13}$
$\tan \theta = \frac{\text{Side opposite to angle }\theta}{\text{Side adjacent to angle }\theta} = \frac{BC}{AB} = \frac{5k}{12k} = \frac{5}{12}$
$\text{cosec } \theta = \frac{\text{Hypotenuse}}{\text{Side opposite to angle }\theta} = \frac{AC}{BC} = \frac{13k}{5k} = \frac{13}{5}$
$\cot \theta = \frac{\text{Side adjacent to angle }\theta}{\text{Side opposite to angle }\theta} = \frac{AB}{BC} = \frac{12k}{5k} = \frac{12}{5}$
The other trigonometric ratios are:
$\sin \theta = \frac{5}{13}$
$\cos \theta = \frac{12}{13}$
$\tan \theta = \frac{5}{12}$
$\text{cosec } \theta = \frac{13}{5}$
$\cot \theta = \frac{12}{5}$
Question 6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Answer:
Given:
$\angle$A and $\angle$B are acute angles.
$\cos$ A = $\cos$ B.
To Show:
$\angle$A = $\angle$B.
Solution:
Consider a right-angled triangle ABC, where $\angle$C is the right angle ($90^\circ$).
In this triangle, A and B are the acute angles.
By the definition of the cosine ratio:
For angle A, $\cos$ A = $\frac{\text{Side adjacent to }\angle\text{A}}{\text{Hypotenuse}} = \frac{AC}{AB}$
For angle B, $\cos$ B = $\frac{\text{Side adjacent to }\angle\text{B}}{\text{Hypotenuse}} = \frac{BC}{AB}$
We are given that $\cos$ A = $\cos$ B.
$\frac{AC}{AB} = \frac{BC}{AB}$
Since AB is the hypotenuse and cannot be zero, we can multiply both sides by AB:
$AC = BC$
AC = BC
(Sides opposite to equal angles)
In $\triangle$ ABC, if two sides are equal (AC = BC), then the angles opposite to these sides are also equal.
The angle opposite to side AC is $\angle$B.
The angle opposite to side BC is $\angle$A.
Therefore,
$\angle$A = $\angle$B
(Angles opposite to equal sides of a triangle are equal)
Since $\angle$A and $\angle$B are given as acute angles, and we have shown they are equal, the condition holds.
Hence Shown.
Alternate Solution (Using Trigonometric Identity/Inverse):
Given $\cos A = \cos B$, where A and B are acute angles.
Since the cosine function is a one-to-one function for acute angles (in the domain $0^\circ \leq \theta \leq 90^\circ$), if $\cos A = \cos B$, then the angles A and B must be equal.
Using the inverse cosine function:
$A = \cos^{-1}(\cos A)$
$B = \cos^{-1}(\cos B)$
Since $\cos A = \cos B$, we have $\cos^{-1}(\cos A) = \cos^{-1}(\cos B)$.
Therefore, $A = B$.
Thus, $\angle$A = $\angle$B.
Hence Shown.
Question 7. If cot θ = $\frac{7}{8}$ , evaluate :
(i) $\frac{(1 \;+\; sin\; θ) (1 \;-\; sin\; θ)}{(1 \;+\; cos\; θ) (1 \;+\; cos\; θ) }$
(ii) cot2 θ
Answer:
Given:
$\cot \theta = \frac{7}{8}$
To Evaluate:
(i) $\frac{(1 + \sin \theta)(1 - \sin \theta)}{(1 + \cos \theta)(1 - \cos \theta)}$
(ii) $\cot^2 \theta$
Solution:
(i) Evaluate $\frac{(1 + \sin \theta)(1 - \sin \theta)}{(1 + \cos \theta)(1 - \cos \theta)}$:
We can simplify the expression using the algebraic identity $(a+b)(a-b) = a^2 - b^2$ in both the numerator and the denominator.
Numerator: $(1 + \sin \theta)(1 - \sin \theta) = 1^2 - \sin^2 \theta = 1 - \sin^2 \theta$
Denominator: $(1 + \cos \theta)(1 - \cos \theta) = 1^2 - \cos^2 \theta = 1 - \cos^2 \theta$
So the expression becomes:
$\frac{1 - \sin^2 \theta}{1 - \cos^2 \theta}$
Using the trigonometric identity $\sin^2 \theta + \cos^2 \theta = 1$, we have:
$1 - \sin^2 \theta = \cos^2 \theta$
$1 - \cos^2 \theta = \sin^2 \theta$
Substitute these into the expression:
$\frac{\cos^2 \theta}{\sin^2 \theta}$
We know that $\frac{\cos \theta}{\sin \theta} = \cot \theta$. Therefore, $\frac{\cos^2 \theta}{\sin^2 \theta} = \left(\frac{\cos \theta}{\sin \theta}\right)^2 = \cot^2 \theta$.
The expression simplifies to $\cot^2 \theta$.
We are given $\cot \theta = \frac{7}{8}$.
So, $\cot^2 \theta = \left(\frac{7}{8}\right)^2 = \frac{7^2}{8^2} = \frac{49}{64}$.
Thus, $\frac{(1 + \sin \theta)(1 - \sin \theta)}{(1 + \cos \theta)(1 - \cos \theta)} = \frac{49}{64}$.
(ii) Evaluate $\cot^2 \theta$:
We are given $\cot \theta = \frac{7}{8}$.
$\cot^2 \theta = (\cot \theta)^2 = \left(\frac{7}{8}\right)^2$
$\cot^2 \theta = \frac{7^2}{8^2} = \frac{49}{64}$
The value of $\cot^2 \theta$ is $\frac{49}{64}$.
Alternate Method for (i) (using a triangle):
Given $\cot \theta = \frac{7}{8}$.
In a right triangle, let the side adjacent to $\theta$ be $7k$ and the side opposite to $\theta$ be $8k$.
Using the Pythagorean theorem, the hypotenuse is $\sqrt{(7k)^2 + (8k)^2} = \sqrt{49k^2 + 64k^2} = \sqrt{113k^2} = k\sqrt{113}$.
Then, $\sin \theta = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{8k}{k\sqrt{113}} = \frac{8}{\sqrt{113}}$.
And $\cos \theta = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{7k}{k\sqrt{113}} = \frac{7}{\sqrt{113}}$.
Now substitute these values into the expression $\frac{(1 + \sin \theta)(1 - \sin \theta)}{(1 + \cos \theta)(1 - \cos \theta)}$:
$\frac{1 - \sin^2 \theta}{1 - \cos^2 \theta} = \frac{1 - \left(\frac{8}{\sqrt{113}}\right)^2}{1 - \left(\frac{7}{\sqrt{113}}\right)^2}$
$= \frac{1 - \frac{64}{113}}{1 - \frac{49}{113}}$
$= \frac{\frac{113 - 64}{113}}{\frac{113 - 49}{113}}$
$= \frac{\frac{49}{113}}{\frac{64}{113}}$
$= \frac{49}{113} \times \frac{113}{64}$
$= \frac{\cancel{113}^{1}}{\cancel{113}_{1}} \times \frac{49}{64} = \frac{49}{64}$
This confirms the result obtained using trigonometric identities.
Question 8. If 3 cot A = 4, check whether $\frac{1\;-\;tan^{2}A}{1\;+\;tan^{2}A}$ = cos2 A - sin2 A or not.
Answer:
Given:
$3 \cot A = 4$
To Check:
Whether $\frac{1 - \tan^2 A}{1 + \tan^2 A} = \cos^2 A - \sin^2 A$ or not.
Solution:
From the given equation, $3 \cot A = 4$, we have:
$\cot A = \frac{4}{3}$
We know that $\tan A = \frac{1}{\cot A}$.
So, $\tan A = \frac{1}{4/3} = \frac{3}{4}$.
Now, let's construct a right-angled triangle ABC, right-angled at B, with respect to angle A.
$\tan A = \frac{\text{Side opposite to A}}{\text{Side adjacent to A}} = \frac{BC}{AB}$
So, $\frac{BC}{AB} = \frac{3}{4}$.
Let $BC = 3k$ and $AB = 4k$, where $k$ is a positive constant.
By the Pythagorean theorem, the hypotenuse AC is:
$AC^2 = AB^2 + BC^2$
$AC^2 = (4k)^2 + (3k)^2$
$AC^2 = 16k^2 + 9k^2$
$AC^2 = 25k^2$
$AC = \sqrt{25k^2} = 5k$ (Since length is positive)
Now we find the values of $\sin A$ and $\cos A$:
$\sin A = \frac{\text{Side opposite to A}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{3k}{5k} = \frac{3}{5}$
$\cos A = \frac{\text{Side adjacent to A}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{4k}{5k} = \frac{4}{5}$
Now, let's evaluate the left side (LHS) of the given equation:
LHS = $\frac{1 - \tan^2 A}{1 + \tan^2 A}$
Substitute the value of $\tan A = \frac{3}{4}$:
LHS = $\frac{1 - (\frac{3}{4})^2}{1 + (\frac{3}{4})^2} = \frac{1 - \frac{9}{16}}{1 + \frac{9}{16}}$
LHS = $\frac{\frac{16 - 9}{16}}{\frac{16 + 9}{16}} = \frac{\frac{7}{16}}{\frac{25}{16}}$
LHS = $\frac{7}{16} \times \frac{16}{25} = \frac{7}{\cancel{16}} \times \frac{\cancel{16}}{25} = \frac{7}{25}$
Now, let's evaluate the right side (RHS) of the given equation:
RHS = $\cos^2 A - \sin^2 A$
Substitute the values of $\cos A = \frac{4}{5}$ and $\sin A = \frac{3}{5}$:
RHS = $\left(\frac{4}{5}\right)^2 - \left(\frac{3}{5}\right)^2$
RHS = $\frac{16}{25} - \frac{9}{25}$
RHS = $\frac{16 - 9}{25} = \frac{7}{25}$
Comparing the LHS and RHS, we see that:
LHS = $\frac{7}{25}$
RHS = $\frac{7}{25}$
Since LHS = RHS, the equality holds true.
Therefore, $\frac{1 - \tan^2 A}{1 + \tan^2 A} = \cos^2 A - \sin^2 A$.
Question 9. In triangle ABC, right-angled at B, if tan A = $\frac{1}{\sqrt{3}}$ find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Answer:
Given:
In $\triangle$ ABC, right-angled at B, $\tan A = \frac{1}{\sqrt{3}}$.
To Find:
(i) $\sin$ A $\cos$ C + $\cos$ A $\sin$ C
(ii) $\cos$ A $\cos$ C – $\sin$ A $\sin$ C
Solution:
We are given $\tan A = \frac{1}{\sqrt{3}}$.
In a right-angled triangle ABC, right-angled at B:
$\tan A = \frac{\text{Side opposite to A}}{\text{Side adjacent to A}} = \frac{BC}{AB}$
So, $\frac{BC}{AB} = \frac{1}{\sqrt{3}}$.
Let $BC = k$ and $AB = k\sqrt{3}$, where $k$ is a positive constant.
By the Pythagorean theorem, the hypotenuse AC is:
$AC^2 = AB^2 + BC^2$
$AC^2 = (k\sqrt{3})^2 + (k)^2$
$AC^2 = 3k^2 + k^2$
$AC^2 = 4k^2$
$AC = \sqrt{4k^2} = 2k$ (Since length is positive)
Now we find the trigonometric ratios for angles A and C.
For angle A:
$\sin A = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{k}{2k} = \frac{1}{2}$
$\cos A = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{k\sqrt{3}}{2k} = \frac{\sqrt{3}}{2}$
For angle C:
The side opposite to angle C is AB.
The side adjacent to angle C is BC.
$\sin C = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{k\sqrt{3}}{2k} = \frac{\sqrt{3}}{2}$
$\cos C = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{k}{2k} = \frac{1}{2}$
(i) Evaluate $\sin$ A $\cos$ C + $\cos$ A $\sin$ C:
Substitute the values we found:
$\sin A \cos C + \cos A \sin C = \left(\frac{1}{2}\right) \times \left(\frac{1}{2}\right) + \left(\frac{\sqrt{3}}{2}\right) \times \left(\frac{\sqrt{3}}{2}\right)$
$= \frac{1}{4} + \frac{(\sqrt{3})^2}{2^2}$
$= \frac{1}{4} + \frac{3}{4}$
$= \frac{1 + 3}{4} = \frac{4}{4} = 1$
So, $\sin A \cos C + \cos A \sin C = 1$.
(ii) Evaluate $\cos$ A $\cos$ C – $\sin$ A $\sin$ C:
Substitute the values we found:
$\cos A \cos C – \sin A \sin C = \left(\frac{\sqrt{3}}{2}\right) \times \left(\frac{1}{2}\right) - \left(\frac{1}{2}\right) \times \left(\frac{\sqrt{3}}{2}\right)$
$= \frac{\sqrt{3}}{4} - \frac{\sqrt{3}}{4}$
$= 0$
So, $\cos A \cos C – \sin A \sin C = 0$.
Alternate Solution (using angles):
Given $\tan A = \frac{1}{\sqrt{3}}$ in a right triangle at B.
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$. Since A is an acute angle, $A = 30^\circ$.
In a right triangle ABC, $\angle A + \angle B + \angle C = 180^\circ$.
$30^\circ + 90^\circ + \angle C = 180^\circ$
$120^\circ + \angle C = 180^\circ$
$\angle C = 180^\circ - 120^\circ = 60^\circ$.
So, $A = 30^\circ$ and $C = 60^\circ$.
Now we find the values of the trigonometric ratios for these angles:
$\sin A = \sin 30^\circ = \frac{1}{2}$
$\cos A = \cos 30^\circ = \frac{\sqrt{3}}{2}$
$\sin C = \sin 60^\circ = \frac{\sqrt{3}}{2}$
$\cos C = \cos 60^\circ = \frac{1}{2}$
(i) Evaluate $\sin$ A $\cos$ C + $\cos$ A $\sin$ C:
$\sin 30^\circ \cos 60^\circ + \cos 30^\circ \sin 60^\circ = \left(\frac{1}{2}\right) \times \left(\frac{1}{2}\right) + \left(\frac{\sqrt{3}}{2}\right) \times \left(\frac{\sqrt{3}}{2}\right)$
$= \frac{1}{4} + \frac{3}{4} = \frac{4}{4} = 1$
(ii) Evaluate $\cos$ A $\cos$ C – $\sin$ A $\sin$ C:
$\cos 30^\circ \cos 60^\circ – \sin 30^\circ \sin 60^\circ = \left(\frac{\sqrt{3}}{2}\right) \times \left(\frac{1}{2}\right) - \left(\frac{1}{2}\right) \times \left(\frac{\sqrt{3}}{2}\right)$
$= \frac{\sqrt{3}}{4} - \frac{\sqrt{3}}{4} = 0$
Question 10. In ∆ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Answer:
Given:
In $\triangle$ PQR, $\angle$Q = $90^\circ$, PQ = 5 cm, PR + QR = 25 cm.
To Find:
The values of $\sin$ P, $\cos$ P, and $\tan$ P.
Solution:
In the right-angled $\triangle$ PQR, by the Pythagorean theorem, we have:
$PR^2 = PQ^2 + QR^2$
We are given PQ = 5 cm and PR + QR = 25 cm.
From the relation PR + QR = 25, we can express PR as:
PR = 25 – QR
Substitute this expression for PR into the Pythagorean theorem:
$(25 – QR)^2 = (5)^2 + QR^2$
Expand the left side using the identity $(a-b)^2 = a^2 - 2ab + b^2$:
$(25)^2 – 2(25)(QR) + QR^2 = 25 + QR^2$
$625 – 50QR + QR^2 = 25 + QR^2$
Subtract $QR^2$ from both sides of the equation:
$625 – 50QR = 25$
Rearrange the terms to solve for QR:
$625 – 25 = 50QR$
$600 = 50QR$
$QR = \frac{600}{50}$
$QR = 12$ cm
Now find the value of PR using the relation PR = 25 – QR:
PR = 25 – 12
PR = 13 cm
So, the lengths of the sides of $\triangle$ PQR are PQ = 5 cm, QR = 12 cm, and PR = 13 cm.
Now, we determine the trigonometric ratios for angle P:
The side opposite to angle P is QR.
The side adjacent to angle P is PQ.
The hypotenuse is PR.
$\sin P = \frac{\text{Side opposite to angle P}}{\text{Hypotenuse}} = \frac{QR}{PR} = \frac{12}{13}$
$\cos P = \frac{\text{Side adjacent to angle P}}{\text{Hypotenuse}} = \frac{PQ}{PR} = \frac{5}{13}$
$\tan P = \frac{\text{Side opposite to angle P}}{\text{Side adjacent to angle P}} = \frac{QR}{PQ} = \frac{12}{5}$
The values are $\sin P = \frac{12}{13}$, $\cos P = \frac{5}{13}$, and $\tan P = \frac{12}{5}$.
Question 11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = $\frac{12}{5}$ for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = $\frac{4}{3}$ for some angle θ.
Answer:
(i) The value of tan A is always less than 1.
False.
Justification:
In a right-angled triangle, $\tan A = \frac{\text{Side opposite to angle A}}{\text{Side adjacent to angle A}}$.
The length of the side opposite to angle A can be greater than, equal to, or less than the length of the side adjacent to angle A, depending on the value of angle A.
For example, if $A = 45^\circ$, the opposite side equals the adjacent side, so $\tan 45^\circ = 1$.
If $A > 45^\circ$ (and $A < 90^\circ$), the side opposite to A is greater than the side adjacent to A, so $\tan A > 1$. For instance, $\tan 60^\circ = \sqrt{3} \approx 1.732$, which is greater than 1.
Therefore, the value of $\tan A$ is not always less than 1.
(ii) sec A = $\frac{12}{5}$ for some value of angle A.
True.
Justification:
In a right-angled triangle, $\sec A = \frac{\text{Hypotenuse}}{\text{Side adjacent to angle A}}$.
The hypotenuse is always the longest side in a right-angled triangle (except for the degenerate case of a right angle with zero area, where sides can be zero, but for an angle in a triangle, sides must be positive). Thus, the ratio of the hypotenuse to the adjacent side must be greater than 1.
Given $\sec A = \frac{12}{5} = 2.4$. Since $2.4 > 1$, this value is a valid value for $\sec A$ for some acute angle A.
We can form a right triangle with adjacent side 5 units and hypotenuse 12 units. By the Pythagorean theorem, the opposite side would be $\sqrt{12^2 - 5^2} = \sqrt{144 - 25} = \sqrt{119}$ units. Since $\sqrt{119}$ is a real positive number, such a triangle exists, and $\sec A = \frac{12}{5}$ is possible.
(iii) cos A is the abbreviation used for the cosecant of angle A.
False.
Justification:
$\cos A$ is the abbreviation used for the cosine of angle A.
The abbreviation used for the cosecant of angle A is $\text{cosec } A$ (or $\text{csc } A$).
(iv) cot A is the product of cot and A.
False.
Justification:
'cot' is part of the trigonometric ratio name 'cotangent'. $\cot A$ represents the cotangent of the angle A. It is not a product of 'cot' and the angle A. The expression $\cot A$ is a single entity representing the ratio of the adjacent side to the opposite side for the angle A in a right triangle.
(v) sin θ = $\frac{4}{3}$ for some angle θ.
False.
Justification:
In a right-angled triangle, $\sin \theta = \frac{\text{Side opposite to angle }\theta}{\text{Hypotenuse}}$.
The length of the side opposite to any angle in a right triangle is always less than or equal to the length of the hypotenuse. Therefore, the ratio $\frac{\text{Opposite}}{\text{Hypotenuse}}$ must be less than or equal to 1.
Given $\sin \theta = \frac{4}{3} \approx 1.33$. Since $1.33 > 1$, this value is not possible for $\sin \theta$ for any real angle $\theta$. The range of the sine function is $[-1, 1]$. For angles in a triangle (which are between $0^\circ$ and $180^\circ$), the value of sine is between 0 and 1 (inclusive).
Example 6 to 8 (Before Exercise 8.2)
Example 6. In ∆ ABC, right-angled at B, AB = 5 cm and ∠ACB = 30° (see Fig. 8.19). Determine the lengths of the sides BC and AC.

Answer:
Given:
In $\triangle$ ABC, $\angle$B = $90^\circ$, AB = 5 cm, and $\angle$ACB = $30^\circ$.
To Determine:
The lengths of the sides BC and AC.
Solution:
We are given a right-angled triangle ABC, with $\angle$B = $90^\circ$, AB = 5 cm, and $\angle$C = $30^\circ$.
We can use trigonometric ratios with respect to the given angle $\angle$C ($30^\circ$) to find the unknown sides.
To find BC (the side adjacent to $\angle$C):
We know the length of the side opposite to $\angle$C (AB = 5 cm). The ratio involving the opposite and adjacent sides is tangent.
$\tan C = \frac{\text{Side opposite to } \angle \text{C}}{\text{Side adjacent to } \angle \text{C}} = \frac{AB}{BC}$
Substitute the given values:
$\tan 30^\circ = \frac{5}{BC}$
We know that the value of $\tan 30^\circ$ is $\frac{1}{\sqrt{3}}$.
$\frac{1}{\sqrt{3}} = \frac{5}{BC}$
Cross-multiply to solve for BC:
$BC \times 1 = 5 \times \sqrt{3}$
$BC = 5\sqrt{3}$ cm
To find AC (the hypotenuse):
We can use the sine ratio, which involves the opposite side and the hypotenuse.
$\sin C = \frac{\text{Side opposite to } \angle \text{C}}{\text{Hypotenuse}} = \frac{AB}{AC}$
Substitute the given values:
$\sin 30^\circ = \frac{5}{AC}$
We know that the value of $\sin 30^\circ$ is $\frac{1}{2}$.
$\frac{1}{2} = \frac{5}{AC}$
Cross-multiply to solve for AC:
$AC \times 1 = 5 \times 2$
$AC = 10$ cm
Alternatively, once BC is found, we could use the cosine ratio for $\angle$C, or the Pythagorean theorem to find AC.
Using $\cos C = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{BC}{AC}$:
$\cos 30^\circ = \frac{5\sqrt{3}}{AC}$
$\frac{\sqrt{3}}{2} = \frac{5\sqrt{3}}{AC}$
$AC \times \sqrt{3} = 2 \times 5\sqrt{3}$
$AC = \frac{10\sqrt{3}}{\sqrt{3}} = 10$ cm.
Using the Pythagorean theorem $AC^2 = AB^2 + BC^2$:
$AC^2 = (5)^2 + (5\sqrt{3})^2$
$AC^2 = 25 + (25 \times 3)$
$AC^2 = 25 + 75$
$AC^2 = 100$
$AC = \sqrt{100} = 10$ cm.
The lengths of the sides are BC = $5\sqrt{3}$ cm and AC = 10 cm.
Example 7. In ∆ PQR, right-angled at Q (see Fig. 8.20), PQ = 3 cm and PR = 6 cm. Determine ∠QPR and ∠PRQ.

Answer:
Given:
In $\triangle$ PQR, $\angle$Q = $90^\circ$, PQ = 3 cm, and PR = 6 cm.
To Determine:
$\angle$QPR and $\angle$PRQ.
Solution:
In the right-angled $\triangle$ PQR, we have PQ = 3 cm and PR = 6 cm. The hypotenuse is PR.
Consider angle P ($\angle$QPR):
The side adjacent to angle P is PQ.
The hypotenuse is PR.
We can use the cosine ratio:
$\cos P = \frac{\text{Side adjacent to P}}{\text{Hypotenuse}} = \frac{PQ}{PR}$
$\cos P = \frac{3}{6} = \frac{1}{2}$
We know that $\cos 60^\circ = \frac{1}{2}$.
Since P is an acute angle in a right triangle, comparing the values, we get:
$P = 60^\circ$
So, $\angle$QPR = $60^\circ$.
Consider angle R ($\angle$PRQ):
The side opposite to angle R is PQ.
The hypotenuse is PR.
We can use the sine ratio:
$\sin R = \frac{\text{Side opposite to R}}{\text{Hypotenuse}} = \frac{PQ}{PR}$
$\sin R = \frac{3}{6} = \frac{1}{2}$
We know that $\sin 30^\circ = \frac{1}{2}$.
Since R is an acute angle in a right triangle, comparing the values, we get:
$R = 30^\circ$
So, $\angle$PRQ = $30^\circ$.
Alternatively, once we found $\angle$P = $60^\circ$, we can find $\angle$R using the angle sum property of a triangle:
In $\triangle$ PQR, $\angle$P + $\angle$Q + $\angle$R = $180^\circ$
$60^\circ + 90^\circ + \angle$R = $180^\circ$
$150^\circ + \angle$R = $180^\circ$
$\angle$R = $180^\circ - 150^\circ = 30^\circ$.
So, $\angle$PRQ = $30^\circ$.
The angles are $\angle$QPR = $60^\circ$ and $\angle$PRQ = $30^\circ$.
Example 8. If sin (A – B) = $\frac{1}{2}$ , cos (A + B) = $\frac{1}{2}$ , 0° < A + B ≤ 90°, A > B, find A and B.
Answer:
Given:
$\sin (A - B) = \frac{1}{2}$
$\cos (A + B) = \frac{1}{2}$
$0^\circ < A + B \leq 90^\circ$
$A > B$
To Find:
The values of angles A and B.
Solution:
We are given the equation $\sin (A - B) = \frac{1}{2}$.
We know that $\sin 30^\circ = \frac{1}{2}$.
Since the sine function is one-to-one for angles in the range typically considered in these problems (especially given A > B and the context of acute angles), we can equate the arguments:
A - B = $30^\circ$
... (i)
We are also given the equation $\cos (A + B) = \frac{1}{2}$.
We know that $\cos 60^\circ = \frac{1}{2}$.
The condition $0^\circ < A + B \leq 90^\circ$ tells us that A + B is an acute angle or a right angle in the first quadrant boundary. Since $\cos (A+B) = \frac{1}{2}$ (which is positive), A + B must be in the first quadrant.
Therefore, we can equate the arguments:
A + B = $60^\circ$
... (ii)
Now we have a system of two linear equations with two variables A and B:
Equation (i): $A - B = 30^\circ$
Equation (ii): $A + B = $60^\circ$
Add equation (i) and equation (ii):
$(A - B) + (A + B) = 30^\circ + 60^\circ$
$2A = 90^\circ$
$A = \frac{90^\circ}{2}$
$A = 45^\circ$
Substitute the value of A into equation (ii):
$45^\circ + B = 60^\circ$
$B = 60^\circ - 45^\circ$
$B = 15^\circ$
Let's check if these values satisfy the given conditions:
$A = 45^\circ$, $B = 15^\circ$.
$A > B$: $45^\circ > 15^\circ$ (True)
$0^\circ < A + B \leq 90^\circ$: $A + B = 45^\circ + 15^\circ = 60^\circ$. $0^\circ < 60^\circ \leq 90^\circ$ (True)
The values of A and B are $45^\circ$ and $15^\circ$ respectively.
Exercise 8.2
Question 1. Evaluate the following :
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan2 45° + cos2 30° – sin2 60°
(iii) $\frac{cos \;45°}{ sec \;30° \;+\; cosec \;30°}$
(iv) $\frac{ sin \;30° \;+\; tan \;45° \;-\; cosec \;60°}{ sec \;30° \;+\; cos\; 60° \;+\; cot\; 45°}$
(v) $\frac{5 cos^2 \;60° \;+\; 4 sec^2 \;30° \;-\; tan^2 \;45°}{sin^2 \;30° \;+\; cos^2 \;30°}$
Answer:
(i) Evaluate $\sin 60^\circ \cos 30^\circ + \sin 30^\circ \cos 60^\circ$:
We use the standard trigonometric values:
$\sin 60^\circ = \frac{\sqrt{3}}{2}$
$\cos 30^\circ = \frac{\sqrt{3}}{2}$
$\sin 30^\circ = \frac{1}{2}$
$\cos 60^\circ = \frac{1}{2}$
Substitute these values into the expression:
$\sin 60^\circ \cos 30^\circ + \sin 30^\circ \cos 60^\circ = \left(\frac{\sqrt{3}}{2}\right) \left(\frac{\sqrt{3}}{2}\right) + \left(\frac{1}{2}\right) \left(\frac{1}{2}\right)$
$= \frac{(\sqrt{3})^2}{2^2} + \frac{1^2}{2^2}$
$= \frac{3}{4} + \frac{1}{4}$
$= \frac{3 + 1}{4} = \frac{4}{4} = 1$
The value is 1.
(ii) Evaluate $2 \tan^2 45^\circ + \cos^2 30^\circ – \sin^2 60^\circ$:
We use the standard trigonometric values:
$\tan 45^\circ = 1$
$\cos 30^\circ = \frac{\sqrt{3}}{2}$
$\sin 60^\circ = \frac{\sqrt{3}}{2}$
Substitute these values into the expression:
$2 \tan^2 45^\circ + \cos^2 30^\circ – \sin^2 60^\circ = 2(1)^2 + \left(\frac{\sqrt{3}}{2}\right)^2 - \left(\frac{\sqrt{3}}{2}\right)^2$
$= 2(1) + \frac{3}{4} - \frac{3}{4}$
$= 2 + 0 = 2$
The value is 2.
(iii) Evaluate $\frac{\cos 45^\circ}{\sec 30^\circ + \text{cosec } 30^\circ}$:
We use the standard trigonometric values:
$\cos 45^\circ = \frac{1}{\sqrt{2}}$
$\sec 30^\circ = \frac{1}{\cos 30^\circ} = \frac{1}{\sqrt{3}/2} = \frac{2}{\sqrt{3}}$
$\text{cosec } 30^\circ = \frac{1}{\sin 30^\circ} = \frac{1}{1/2} = 2$
Substitute these values into the expression:
$\frac{\cos 45^\circ}{\sec 30^\circ + \text{cosec } 30^\circ} = \frac{\frac{1}{\sqrt{2}}}{\frac{2}{\sqrt{3}} + 2}$
Find a common denominator in the denominator:
$= \frac{\frac{1}{\sqrt{2}}}{\frac{2 + 2\sqrt{3}}{\sqrt{3}}}$
Invert the denominator and multiply:
$= \frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{2 + 2\sqrt{3}}$
$= \frac{\sqrt{3}}{\sqrt{2}(2 + 2\sqrt{3})}$
$= \frac{\sqrt{3}}{2\sqrt{2} + 2\sqrt{6}}$
Rationalize the denominator by multiplying the numerator and denominator by the conjugate of the denominator, which is $2\sqrt{2} - 2\sqrt{6}$ or $2(\sqrt{2} - \sqrt{6})$. It's simpler to factor out 2 first.
$= \frac{\sqrt{3}}{2(\sqrt{2} + \sqrt{6})}$
Now multiply by $\frac{\sqrt{6}-\sqrt{2}}{\sqrt{6}-\sqrt{2}}$ (conjugate of $\sqrt{2} + \sqrt{6}$ after swapping terms for easier calculation of difference of squares):
$= \frac{\sqrt{3}(\sqrt{6}-\sqrt{2})}{2(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})}$
$= \frac{\sqrt{18}-\sqrt{6}}{2((\sqrt{6})^2-(\sqrt{2})^2)}$
$= \frac{\sqrt{9 \times 2}-\sqrt{6}}{2(6-2)}$
$= \frac{3\sqrt{2}-\sqrt{6}}{2(4)}$
$= \frac{3\sqrt{2}-\sqrt{6}}{8}$
The value is $\frac{3\sqrt{2}-\sqrt{6}}{8}$.
(iv) Evaluate $\frac{\sin 30^\circ + \tan 45^\circ – \text{cosec } 60^\circ}{\sec 30^\circ + \cos 60^\circ + \cot 45^\circ}$:
We use the standard trigonometric values:
$\sin 30^\circ = \frac{1}{2}$
$\tan 45^\circ = 1$
$\text{cosec } 60^\circ = \frac{1}{\sin 60^\circ} = \frac{1}{\sqrt{3}/2} = \frac{2}{\sqrt{3}}$
$\sec 30^\circ = \frac{1}{\cos 30^\circ} = \frac{1}{\sqrt{3}/2} = \frac{2}{\sqrt{3}}$
$\cos 60^\circ = \frac{1}{2}$
$\cot 45^\circ = 1$
Substitute these values into the expression:
Numerator = $\sin 30^\circ + \tan 45^\circ – \text{cosec } 60^\circ = \frac{1}{2} + 1 - \frac{2}{\sqrt{3}}$
$= \frac{1}{2} + \frac{2}{2} - \frac{2}{\sqrt{3}} = \frac{3}{2} - \frac{2}{\sqrt{3}}$
Find a common denominator: $\frac{3\sqrt{3} - 4}{2\sqrt{3}}$
Denominator = $\sec 30^\circ + \cos 60^\circ + \cot 45^\circ = \frac{2}{\sqrt{3}} + \frac{1}{2} + 1$
$= \frac{2}{\sqrt{3}} + \frac{1}{2} + \frac{2}{2} = \frac{2}{\sqrt{3}} + \frac{3}{2}$
Find a common denominator: $\frac{4 + 3\sqrt{3}}{2\sqrt{3}}$
Now divide the numerator by the denominator:
$\frac{\frac{3\sqrt{3} - 4}{2\sqrt{3}}}{\frac{4 + 3\sqrt{3}}{2\sqrt{3}}} = \frac{3\sqrt{3} - 4}{2\sqrt{3}} \times \frac{2\sqrt{3}}{4 + 3\sqrt{3}}$
$= \frac{3\sqrt{3} - 4}{\cancel{2\sqrt{3}}} \times \frac{\cancel{2\sqrt{3}}}{3\sqrt{3} + 4}$
$= \frac{3\sqrt{3} - 4}{3\sqrt{3} + 4}$
Rationalize the denominator by multiplying the numerator and denominator by the conjugate of the denominator, which is $3\sqrt{3} - 4$:
$= \frac{(3\sqrt{3} - 4)(3\sqrt{3} - 4)}{(3\sqrt{3} + 4)(3\sqrt{3} - 4)}$
Use $(a-b)^2 = a^2 - 2ab + b^2$ for the numerator and $(a+b)(a-b) = a^2 - b^2$ for the denominator:
Numerator = $(3\sqrt{3})^2 - 2(3\sqrt{3})(4) + (4)^2 = (9 \times 3) - 24\sqrt{3} + 16 = 27 - 24\sqrt{3} + 16 = 43 - 24\sqrt{3}$
Denominator = $(3\sqrt{3})^2 - (4)^2 = (9 \times 3) - 16 = 27 - 16 = 11$
The expression is equal to $\frac{43 - 24\sqrt{3}}{11}$.
(v) Evaluate $\frac{5 \cos^2 60^\circ + 4 \sec^2 30^\circ – \tan^2 45^\circ}{\sin^2 30^\circ + \cos^2 30^\circ}$:
We use the standard trigonometric values:
$\cos 60^\circ = \frac{1}{2}$
$\sec 30^\circ = \frac{2}{\sqrt{3}}$
$\tan 45^\circ = 1$
$\sin 30^\circ = \frac{1}{2}$
$\cos 30^\circ = \frac{\sqrt{3}}{2}$
Substitute these values into the expression:
Numerator = $5 \cos^2 60^\circ + 4 \sec^2 30^\circ – \tan^2 45^\circ = 5\left(\frac{1}{2}\right)^2 + 4\left(\frac{2}{\sqrt{3}}\right)^2 - (1)^2$
$= 5\left(\frac{1}{4}\right) + 4\left(\frac{4}{3}\right) - 1$
$= \frac{5}{4} + \frac{16}{3} - 1$
Find a common denominator (12):
$= \frac{5 \times 3}{4 \times 3} + \frac{16 \times 4}{3 \times 4} - \frac{1 \times 12}{12}$
$= \frac{15}{12} + \frac{64}{12} - \frac{12}{12}$
$= \frac{15 + 64 - 12}{12} = \frac{79 - 12}{12} = \frac{67}{12}$
Denominator = $\sin^2 30^\circ + \cos^2 30^\circ = \left(\frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2$
$= \frac{1}{4} + \frac{3}{4} = \frac{1+3}{4} = \frac{4}{4} = 1$
Alternatively, using the identity $\sin^2 \theta + \cos^2 \theta = 1$, the denominator is simply 1.
Now divide the numerator by the denominator:
$\frac{\frac{67}{12}}{1} = \frac{67}{12}$
The value is $\frac{67}{12}$.
Question 2. Choose the correct option and justify your choice :
(i) $\frac{2 tan\; 30°}{1 \;+\; tan^{2}\;30°}$ =
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sin 30°
(ii) $\frac{1 \;-\; tan^{2}\;45°}{1 \;+\; tan^{2}\;45°}$ =
(A) tan 90°
(B) 1
(C) sin 45°
(D) 0
(iii) sin 2A = 2 sin A is true when A =
(A) 0°
(B) 30°
(C) 45°
(D) 60°
(iv) $\frac{2tan \;30° }{1 \;-\; tan^{2}\;30° }$ =
(A) cos 60°
(B) sin 60°
(C) tan 60°
(D) sin 30°
Answer:
(i) $\frac{2 \tan 30^\circ}{1 + \tan^2 30^\circ}$:
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
Substitute this value into the expression:
$\frac{2 (\frac{1}{\sqrt{3}})}{1 + (\frac{1}{\sqrt{3}})^2} = \frac{\frac{2}{\sqrt{3}}}{1 + \frac{1}{3}}$
$= \frac{\frac{2}{\sqrt{3}}}{\frac{3+1}{3}} = \frac{\frac{2}{\sqrt{3}}}{\frac{4}{3}}$
$= \frac{2}{\sqrt{3}} \times \frac{3}{4}$
$= \frac{\cancel{2}^1}{\sqrt{3}} \times \frac{3}{\cancel{4}^2} = \frac{3}{2\sqrt{3}}$
Rationalize the denominator:
$= \frac{3}{2\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{3\sqrt{3}}{2(3)} = \frac{\cancel{3}\sqrt{3}}{2\cancel{3}} = \frac{\sqrt{3}}{2}$
Now, we compare this value with the given options:
(A) $\sin 60^\circ = \frac{\sqrt{3}}{2}$
(B) $\cos 60^\circ = \frac{1}{2}$
(C) $\tan 60^\circ = \sqrt{3}$
(D) $\sin 30^\circ = \frac{1}{2}$
The value of the expression is equal to $\sin 60^\circ$.
The correct option is (A).
Justification: Calculation shows the expression evaluates to $\frac{\sqrt{3}}{2}$, which is the value of $\sin 60^\circ$.
(ii) $\frac{1 - \tan^2 45^\circ}{1 + \tan^2 45^\circ}$:
We know that $\tan 45^\circ = 1$.
Substitute this value into the expression:
$\frac{1 - (1)^2}{1 + (1)^2} = \frac{1 - 1}{1 + 1} = \frac{0}{2} = 0$
Now, we compare this value with the given options:
(A) $\tan 90^\circ$ (Undefined)
(B) 1
(C) $\sin 45^\circ = \frac{1}{\sqrt{2}}$
(D) 0
The value of the expression is 0.
The correct option is (D).
Justification: Calculation shows the expression evaluates to 0.
(iii) $\sin 2A = 2 \sin A$ is true when A =:
We need to check which value of A satisfies the equation $\sin 2A = 2 \sin A$.
(A) If $A = 0^\circ$:
LHS = $\sin (2 \times 0^\circ) = \sin 0^\circ = 0$
RHS = $2 \sin 0^\circ = 2 \times 0 = 0$
LHS = RHS. So, A = $0^\circ$ is a solution.
(B) If $A = 30^\circ$:
LHS = $\sin (2 \times 30^\circ) = \sin 60^\circ = \frac{\sqrt{3}}{2}$
RHS = $2 \sin 30^\circ = 2 \times \frac{1}{2} = 1$
LHS $\neq$ RHS.
(C) If $A = 45^\circ$:
LHS = $\sin (2 \times 45^\circ) = \sin 90^\circ = 1$
RHS = $2 \sin 45^\circ = 2 \times \frac{1}{\sqrt{2}} = \sqrt{2}$
LHS $\neq$ RHS.
(D) If $A = 60^\circ$:
LHS = $\sin (2 \times 60^\circ) = \sin 120^\circ$. $\sin 120^\circ = \sin(180^\circ - 60^\circ) = \sin 60^\circ = \frac{\sqrt{3}}{2}$
RHS = $2 \sin 60^\circ = 2 \times \frac{\sqrt{3}}{2} = \sqrt{3}$
LHS $\neq$ RHS.
The equation $\sin 2A = 2 \sin A$ is true only when $A = 0^\circ$ (or other values not typically covered in basic trigonometry). Based on the options provided, only A = $0^\circ$ satisfies the condition.
The correct option is (A).
Justification: We checked each option and found that only A = $0^\circ$ satisfies the equation $\sin 2A = 2 \sin A$. (Using the double angle identity $\sin 2A = 2 \sin A \cos A$, the equation becomes $2 \sin A \cos A = 2 \sin A$, which simplifies to $2 \sin A \cos A - 2 \sin A = 0$, or $2 \sin A (\cos A - 1) = 0$. This is true if $\sin A = 0$ or $\cos A = 1$. Both occur when $A = 0^\circ$.)
(iv) $\frac{2 \tan 30^\circ}{1 - \tan^2 30^\circ}$:
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
Substitute this value into the expression:
$\frac{2 (\frac{1}{\sqrt{3}})}{1 - (\frac{1}{\sqrt{3}})^2} = \frac{\frac{2}{\sqrt{3}}}{1 - \frac{1}{3}}$
$= \frac{\frac{2}{\sqrt{3}}}{\frac{3-1}{3}} = \frac{\frac{2}{\sqrt{3}}}{\frac{2}{3}}$
$= \frac{2}{\sqrt{3}} \times \frac{3}{2}$
$= \frac{\cancel{2}}{\sqrt{3}} \times \frac{3}{\cancel{2}} = \frac{3}{\sqrt{3}}$
Rationalize the denominator:
$= \frac{3}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{3\sqrt{3}}{3} = \sqrt{3}$
Now, we compare this value with the given options:
(A) $\cos 60^\circ = \frac{1}{2}$
(B) $\sin 60^\circ = \frac{\sqrt{3}}{2}$
(C) $\tan 60^\circ = \sqrt{3}$
(D) $\sin 30^\circ = \frac{1}{2}$
The value of the expression is equal to $\tan 60^\circ$.
The correct option is (C).
Justification: Calculation shows the expression evaluates to $\sqrt{3}$, which is the value of $\tan 60^\circ$. (This expression is also the formula for $\tan 2A$, so $\tan(2 \times 30^\circ) = \tan 60^\circ$).
Question 3. If tan (A + B) = $\sqrt{3}$ and tan (A – B) = $\frac{1}{\sqrt{3}}$ ; 0° < A + B ≤ 90°; A > B, find A and B.
Answer:
Given:
$\tan (A + B) = \sqrt{3}$
$\tan (A - B) = \frac{1}{\sqrt{3}}$
$0^\circ < A + B \leq 90^\circ$
$A > B$
To Find:
The values of angles A and B.
Solution:
We are given the equation $\tan (A + B) = \sqrt{3}$.
We know that $\tan 60^\circ = \sqrt{3}$.
Given that $0^\circ < A + B \leq 90^\circ$, and the tangent is positive, A + B must be in the first quadrant. The unique angle in this range whose tangent is $\sqrt{3}$ is $60^\circ$.
Therefore, we can equate the arguments:
A + B = $60^\circ$
... (i)
We are also given the equation $\tan (A - B) = \frac{1}{\sqrt{3}}$.
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
Given that $A > B$, the difference $A - B$ must be positive. Also, since $A+B \leq 90^\circ$ and $B > 0$ (otherwise $A=A+B$ and $\tan A = \sqrt{3}$ would mean $A=60^\circ$, then $B=0$, and $\tan(60-0) = \tan 60 = \sqrt{3} \neq 1/\sqrt{3}$), it implies $A < 90^\circ$ and $B$ is also an acute angle, making $A-B$ also likely acute. The unique angle whose tangent is $\frac{1}{\sqrt{3}}$ is $30^\circ$.
Therefore, we can equate the arguments:
A - B = $30^\circ$
... (ii)
Now we have a system of two linear equations with two variables A and B:
From equation (i): $A + B = 60^\circ$
From equation (ii): $A - B = 30^\circ$
Add equation (i) and equation (ii):
$(A + B) + (A - B) = 60^\circ + 30^\circ$
$2A = 90^\circ$
$A = \frac{90^\circ}{2}$
A = $45^\circ$
Substitute the value of A = $45^\circ$ into equation (i):
$45^\circ + B = 60^\circ$
$B = 60^\circ - 45^\circ$
B = $15^\circ$
Let's verify if these values satisfy the given conditions:
$A = 45^\circ$ and $B = 15^\circ$.
$A > B$: $45^\circ > 15^\circ$. This condition is satisfied.
$0^\circ < A + B \leq 90^\circ$: $A + B = 45^\circ + 15^\circ = 60^\circ$. $0^\circ < 60^\circ \leq 90^\circ$. This condition is satisfied.
The values of A and B are $45^\circ$ and $15^\circ$ respectively.
Question 4. State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Answer:
(i) $\sin (A + B) = \sin A + \sin B$.
False.
Justification:
Consider A = $30^\circ$ and B = $60^\circ$.
LHS = $\sin (A + B) = \sin (30^\circ + 60^\circ) = \sin 90^\circ = 1$.
RHS = $\sin A + \sin B = \sin 30^\circ + \sin 60^\circ = \frac{1}{2} + \frac{\sqrt{3}}{2} = \frac{1+\sqrt{3}}{2}$.
Since $1 \neq \frac{1+\sqrt{3}}{2}$, the statement $\sin (A + B) = \sin A + \sin B$ is generally false.
(ii) The value of $\sin \theta$ increases as $\theta$ increases.
True (for $0^\circ \leq \theta \leq 90^\circ$).
Justification:
Consider the values of $\sin \theta$ for increasing $\theta$ in the range from $0^\circ$ to $90^\circ$ (which is the typical range for angles in a right triangle as considered in this chapter):
$\sin 0^\circ = 0$
$\sin 30^\circ = 0.5$
$\sin 45^\circ = \frac{1}{\sqrt{2}} \approx 0.707$
$\sin 60^\circ = \frac{\sqrt{3}}{2} \approx 0.866$
$\sin 90^\circ = 1$
As $\theta$ increases from $0^\circ$ to $90^\circ$, the value of $\sin \theta$ monotonically increases from 0 to 1. Therefore, the statement is true for this range of $\theta$.
(iii) The value of $\cos \theta$ increases as $\theta$ increases.
False.
Justification:
Consider the values of $\cos \theta$ for increasing $\theta$ in the range from $0^\circ$ to $90^\circ$:
$\cos 0^\circ = 1$
$\cos 30^\circ = \frac{\sqrt{3}}{2} \approx 0.866$
$\cos 45^\circ = \frac{1}{\sqrt{2}} \approx 0.707$
$\cos 60^\circ = 0.5$
$\cos 90^\circ = 0$
As $\theta$ increases from $0^\circ$ to $90^\circ$, the value of $\cos \theta$ monotonically decreases from 1 to 0. Therefore, the statement is false for this range of $\theta$.
(iv) $\sin \theta = \cos \theta$ for all values of $\theta$.
False.
Justification:
The equality $\sin \theta = \cos \theta$ is only true for specific values of $\theta$, such as $\theta = 45^\circ$ (or $45^\circ + n \times 180^\circ$, where $n$ is an integer). It is not true for all values of $\theta$.
For example, if $\theta = 30^\circ$, $\sin 30^\circ = \frac{1}{2}$ and $\cos 30^\circ = \frac{\sqrt{3}}{2}$. Since $\frac{1}{2} \neq \frac{\sqrt{3}}{2}$, the statement is false.
(v) $\cot A$ is not defined for $A = 0^\circ$.
True.
Justification:
The trigonometric ratio $\cot A$ is defined as $\cot A = \frac{\cos A}{\sin A}$.
For $A = 0^\circ$, we have $\cos 0^\circ = 1$ and $\sin 0^\circ = 0$.
So, $\cot 0^\circ = \frac{\cos 0^\circ}{\sin 0^\circ} = \frac{1}{0}$.
Division by zero is undefined. Therefore, $\cot A$ is not defined for $A = 0^\circ$.
Example 9 to 11 (Before Exercise 8.3)
Example 9. Evaluate $\frac{\tan 65^\circ}{\cot 25^\circ}$
Answer:
To Evaluate:
$\frac{\tan 65^\circ}{\cot 25^\circ}$
Solution:
We use the trigonometric identity for complementary angles: $\tan (90^\circ - \theta) = \cot \theta$ and $\cot (90^\circ - \theta) = \tan \theta$.
Notice that $65^\circ + 25^\circ = 90^\circ$. So, $65^\circ$ and $25^\circ$ are complementary angles.
We can write $65^\circ = 90^\circ - 25^\circ$.
So, $\tan 65^\circ = \tan (90^\circ - 25^\circ)$.
Using the identity $\tan (90^\circ - \theta) = \cot \theta$ with $\theta = 25^\circ$, we get:
$\tan 65^\circ = \cot 25^\circ$
Alternatively, we can write $25^\circ = 90^\circ - 65^\circ$.
So, $\cot 25^\circ = \cot (90^\circ - 65^\circ)$.
Using the identity $\cot (90^\circ - \theta) = \tan \theta$ with $\theta = 65^\circ$, we get:
$\cot 25^\circ = \tan 65^\circ$
Now, substitute either of these results back into the expression:
$\frac{\tan 65^\circ}{\cot 25^\circ} = \frac{\cot 25^\circ}{\cot 25^\circ} = 1$ (using $\tan 65^\circ = \cot 25^\circ$)
or
$\frac{\tan 65^\circ}{\cot 25^\circ} = \frac{\tan 65^\circ}{\tan 65^\circ} = 1$ (using $\cot 25^\circ = \tan 65^\circ$)
The value of the expression is 1.
Example 10. If sin 3A = cos (A – 26°), where 3A is an acute angle, find the value of A.
Answer:
Given:
$\sin 3A = \cos (A – 26^\circ)$
3A is an acute angle ($0^\circ < 3A < 90^\circ$).
To Find:
The value of A.
Solution:
We are given the equation $\sin 3A = \cos (A – 26^\circ)$.
We use the identity $\sin \theta = \cos (90^\circ - \theta)$.
Since 3A is an acute angle, we can write $\sin 3A$ as $\cos (90^\circ - 3A)$.
Substitute this into the given equation:
$\cos (90^\circ - 3A) = \cos (A – 26^\circ)$
Since both angles are likely acute (or within the range where cosine is one-to-one or its values correspond uniquely to acute angles in this context), we can equate the arguments:
$90^\circ - 3A = A – 26^\circ$
Rearrange the terms to solve for A:
$90^\circ + 26^\circ = A + 3A$
$116^\circ = 4A$
$A = \frac{116^\circ}{4}$
$A = 29^\circ$
Let's check if the conditions are satisfied with A = $29^\circ$:
3A = $3 \times 29^\circ = 87^\circ$. This is an acute angle ($0^\circ < 87^\circ < 90^\circ$), so the condition is satisfied.
A – $26^\circ = 29^\circ – 26^\circ = 3^\circ$. This angle is also acute and positive.
With $A = 29^\circ$, the original equation is $\sin 87^\circ = \cos 3^\circ$. This is true because $\sin 87^\circ = \sin (90^\circ - 3^\circ) = \cos 3^\circ$.
The value of A is $29^\circ$.
Example 11. Express cot 85° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Answer:
To Express:
$\cot 85^\circ + \cos 75^\circ$ in terms of trigonometric ratios of angles between $0^\circ$ and $45^\circ$.
Solution:
We need to express the given trigonometric ratios of angles $85^\circ$ and $75^\circ$ (which are greater than $45^\circ$) in terms of trigonometric ratios of angles between $0^\circ$ and $45^\circ$.
We use the complementary angle identities:
$\cot \theta = \tan (90^\circ - \theta)$
$\cos \theta = \sin (90^\circ - \theta)$
For the term $\cot 85^\circ$:
The angle is $85^\circ$. The complementary angle is $90^\circ - 85^\circ = 5^\circ$.
$\cot 85^\circ = \cot (90^\circ - 5^\circ) = \tan 5^\circ$
The angle $5^\circ$ is between $0^\circ$ and $45^\circ$.
For the term $\cos 75^\circ$:
The angle is $75^\circ$. The complementary angle is $90^\circ - 75^\circ = 15^\circ$.
$\cos 75^\circ = \cos (90^\circ - 15^\circ) = \sin 15^\circ$
The angle $15^\circ$ is between $0^\circ$ and $45^\circ$.
Now, substitute these expressions back into the original sum:
$\cot 85^\circ + \cos 75^\circ = \tan 5^\circ + \sin 15^\circ$
The expression $\cot 85^\circ + \cos 75^\circ$ is expressed in terms of trigonometric ratios of angles $5^\circ$ and $15^\circ$, both of which are between $0^\circ$ and $45^\circ$.
The expression is $\tan 5^\circ + \sin 15^\circ$.
Exercise 8.3
Question 1. Evaluate :
(i) $\frac{sin \;18°}{cos \;72°}$
(ii) $\frac{tan \;26°}{cot \;64°}$
(iii) cos 48° – sin 42°
(iv) cosec 31° – sec 59°
Answer:
(i) Evaluate $\frac{\sin 18^\circ}{\cos 72^\circ}$:
We notice that $18^\circ + 72^\circ = 90^\circ$. These are complementary angles.
We use the identity $\sin (90^\circ - \theta) = \cos \theta$ or $\cos (90^\circ - \theta) = \sin \theta$.
Let's express the numerator in terms of cosine:
$\sin 18^\circ = \sin (90^\circ - 72^\circ) = \cos 72^\circ$
Substitute this into the expression:
$\frac{\sin 18^\circ}{\cos 72^\circ} = \frac{\cos 72^\circ}{\cos 72^\circ}$
Assuming $\cos 72^\circ \neq 0$, which is true since $0^\circ < 72^\circ < 90^\circ$, we can cancel the terms.
$= 1$
Alternatively, express the denominator in terms of sine:
$\cos 72^\circ = \cos (90^\circ - 18^\circ) = \sin 18^\circ$
Substitute this into the expression:
$\frac{\sin 18^\circ}{\cos 72^\circ} = \frac{\sin 18^\circ}{\sin 18^\circ}$
Assuming $\sin 18^\circ \neq 0$, which is true since $0^\circ < 18^\circ < 90^\circ$, we can cancel the terms.
$= 1$
The value is 1.
(ii) Evaluate $\frac{\tan 26^\circ}{\cot 64^\circ}$:
We notice that $26^\circ + 64^\circ = 90^\circ$. These are complementary angles.
We use the identity $\tan (90^\circ - \theta) = \cot \theta$ or $\cot (90^\circ - \theta) = \tan \theta$.
Let's express the numerator in terms of cotangent:
$\tan 26^\circ = \tan (90^\circ - 64^\circ) = \cot 64^\circ$
Substitute this into the expression:
$\frac{\tan 26^\circ}{\cot 64^\circ} = \frac{\cot 64^\circ}{\cot 64^\circ}$
Assuming $\cot 64^\circ \neq 0$, which is true since $0^\circ < 64^\circ < 90^\circ$, we can cancel the terms.
$= 1$
The value is 1.
(iii) Evaluate $\cos 48^\circ – \sin 42^\circ$:
We notice that $48^\circ + 42^\circ = 90^\circ$. These are complementary angles.
We use the identity $\cos (90^\circ - \theta) = \sin \theta$ or $\sin (90^\circ - \theta) = \cos \theta$.
Let's express the first term in terms of sine:
$\cos 48^\circ = \cos (90^\circ - 42^\circ) = \sin 42^\circ$
Substitute this into the expression:
$\cos 48^\circ – \sin 42^\circ = \sin 42^\circ – \sin 42^\circ$
$= 0$
Alternatively, express the second term in terms of cosine:
$\sin 42^\circ = \sin (90^\circ - 48^\circ) = \cos 48^\circ$
Substitute this into the expression:
$\cos 48^\circ – \sin 42^\circ = \cos 48^\circ – \cos 48^\circ$
$= 0$
The value is 0.
(iv) Evaluate $\text{cosec } 31^\circ – \sec 59^\circ$:
We notice that $31^\circ + 59^\circ = 90^\circ$. These are complementary angles.
We use the identity $\text{cosec } (90^\circ - \theta) = \sec \theta$ or $\sec (90^\circ - \theta) = \text{cosec } \theta$.
Let's express the first term in terms of secant:
$\text{cosec } 31^\circ = \text{cosec } (90^\circ - 59^\circ) = \sec 59^\circ$
Substitute this into the expression:
$\text{cosec } 31^\circ – \sec 59^\circ = \sec 59^\circ – \sec 59^\circ$
$= 0$
Alternatively, express the second term in terms of cosecant:
$\sec 59^\circ = \sec (90^\circ - 31^\circ) = \text{cosec } 31^\circ$
Substitute this into the expression:
$\text{cosec } 31^\circ – \sec 59^\circ = \text{cosec } 31^\circ – \text{cosec } 31^\circ$
$= 0$
The value is 0.
Question 2. Show that :
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
Answer:
(i) Show that $\tan 48^\circ \tan 23^\circ \tan 42^\circ \tan 67^\circ = 1$:
Consider the Left Hand Side (LHS):
LHS = $\tan 48^\circ \tan 23^\circ \tan 42^\circ \tan 67^\circ$
Group the terms that are complementary:
Notice that $48^\circ + 42^\circ = 90^\circ$ and $23^\circ + 67^\circ = 90^\circ$.
We use the identity $\tan (90^\circ - \theta) = \cot \theta$.
$\tan 48^\circ = \tan (90^\circ - 42^\circ) = \cot 42^\circ$
$\tan 23^\circ = \tan (90^\circ - 67^\circ) = \cot 67^\circ$
Substitute these into the LHS:
LHS = $(\cot 42^\circ) (\cot 67^\circ) (\tan 42^\circ) (\tan 67^\circ)$
Rearrange the terms:
LHS = $(\cot 42^\circ \tan 42^\circ) (\cot 67^\circ \tan 67^\circ)$
We know that $\cot \theta \tan \theta = 1$ (since $\cot \theta = \frac{1}{\tan \theta}$).
LHS = $(1) \times (1)$
LHS = 1
This is equal to the Right Hand Side (RHS).
Hence Shown.
(ii) Show that $\cos 38^\circ \cos 52^\circ – \sin 38^\circ \sin 52^\circ = 0$:
Consider the Left Hand Side (LHS):
LHS = $\cos 38^\circ \cos 52^\circ – \sin 38^\circ \sin 52^\circ$
Notice that $38^\circ + 52^\circ = 90^\circ$. These are complementary angles.
We use the identity $\sin (90^\circ - \theta) = \cos \theta$ and $\cos (90^\circ - \theta) = \sin \theta$.
Let's express the terms involving $52^\circ$ in terms of $38^\circ$:
$\cos 52^\circ = \cos (90^\circ - 38^\circ) = \sin 38^\circ$
$\sin 52^\circ = \sin (90^\circ - 38^\circ) = \cos 38^\circ$
Substitute these into the LHS:
LHS = $\cos 38^\circ (\sin 38^\circ) – \sin 38^\circ (\cos 38^\circ)$
LHS = $\cos 38^\circ \sin 38^\circ – \sin 38^\circ \cos 38^\circ$
The two terms are identical but with opposite signs, so they cancel out.
LHS = 0
This is equal to the Right Hand Side (RHS).
Hence Shown.
Alternate Solution for (ii) (using angle sum identity):
Recall the cosine addition formula: $\cos (A + B) = \cos A \cos B - \sin A \sin B$.
The expression $\cos 38^\circ \cos 52^\circ – \sin 38^\circ \sin 52^\circ$ matches the form of $\cos (A + B)$ with $A = 38^\circ$ and $B = 52^\circ$.
LHS = $\cos (38^\circ + 52^\circ)$
LHS = $\cos 90^\circ$
We know that $\cos 90^\circ = 0$.
LHS = 0
This is equal to the RHS.
Hence Shown.
Question 3. If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Answer:
Given:
$\tan 2A = \cot (A – 18^\circ)$
2A is an acute angle ($0^\circ < 2A < 90^\circ$).
To Find:
The value of A.
Solution:
We are given the equation $\tan 2A = \cot (A – 18^\circ)$.
We know the trigonometric identity for complementary angles: $\tan \theta = \cot (90^\circ - \theta)$.
Since 2A is an acute angle, we can write $\tan 2A$ as $\cot (90^\circ - 2A)$.
Substitute this into the given equation:
$\cot (90^\circ - 2A) = \cot (A – 18^\circ)$
Since $2A$ is an acute angle, $90^\circ - 2A$ is also an angle between $0^\circ$ and $90^\circ$. For these angles, the cotangent function is one-to-one. Thus, we can equate the arguments of the cotangent function:
$90^\circ - 2A = A – 18^\circ$
Now, we solve this linear equation for A.
Add $2A$ to both sides:
$90^\circ = A – 18^\circ + 2A$
$90^\circ = 3A – 18^\circ$
Add $18^\circ$ to both sides:
$90^\circ + 18^\circ = 3A$
$108^\circ = 3A$
Divide by 3:
$A = \frac{108^\circ}{3}$
$A = 36^\circ$
Let's verify the condition that 2A is an acute angle:
$2A = 2 \times 36^\circ = 72^\circ$. Since $0^\circ < 72^\circ < 90^\circ$, 2A is indeed an acute angle.
Also, $A - 18^\circ = 36^\circ - 18^\circ = 18^\circ$, which is positive.
The value of A is $36^\circ$.
Question 4. If tan A = cot B, prove that A + B = 90°.
Answer:
Given:
$\tan A = \cot B$
Angles A and B are acute angles (implied by the context of trigonometric ratios in a right triangle in this section).
To Prove:
A + B = $90^\circ$.
Solution:
We are given the equation $\tan A = \cot B$.
We use the trigonometric identity for complementary angles: $\cot \theta = \tan (90^\circ - \theta)$.
We can rewrite the right side of the given equation using this identity:
$\cot B = \tan (90^\circ - B)$
Substitute this back into the given equation:
$\tan A = \tan (90^\circ - B)$
Since A and B are acute angles (and thus $90^\circ - B$ is also an angle between $0^\circ$ and $90^\circ$), and the tangent function is one-to-one for angles between $0^\circ$ and $90^\circ$, we can equate the arguments:
$A = 90^\circ - B$
Add B to both sides of the equation:
$A + B = 90^\circ$
Thus, if $\tan A = \cot B$ and A and B are acute angles, then A + B = $90^\circ$.
Hence Proved.
Alternate Solution:
We are given $\tan A = \cot B$.
We can use the identity $\tan A = \frac{\sin A}{\cos A}$ and $\cot B = \frac{\cos B}{\sin B}$.
$\frac{\sin A}{\cos A} = \frac{\cos B}{\sin B}$
Cross-multiply:
$\sin A \sin B = \cos A \cos B$
Rearrange the terms:
$\cos A \cos B - \sin A \sin B = 0$
Recognize the left side as the cosine addition formula $\cos (A + B) = \cos A \cos B - \sin A \sin B$:
$\cos (A + B) = 0$
For acute angles A and B, A + B will be in the range $(0^\circ, 180^\circ)$. The angle in this range whose cosine is 0 is $90^\circ$.
Therefore, $A + B = 90^\circ$.
Hence Proved.
Question 5. If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Answer:
Given:
$\sec 4A = \text{cosec } (A – 20^\circ)$
4A is an acute angle ($0^\circ < 4A < 90^\circ$).
To Find:
The value of A.
Solution:
We are given the equation $\sec 4A = \text{cosec } (A – 20^\circ)$.
We use the trigonometric identity for complementary angles: $\sec \theta = \text{cosec } (90^\circ - \theta)$ or $\text{cosec } \theta = \sec (90^\circ - \theta)$.
Since 4A is an acute angle, we can write $\sec 4A$ as $\text{cosec } (90^\circ - 4A)$.
Substitute this into the given equation:
$\text{cosec } (90^\circ - 4A) = \text{cosec } (A – 20^\circ)$
Since $4A$ is an acute angle, $90^\circ - 4A$ is also an angle between $0^\circ$ and $90^\circ$. For these angles, the cosecant function is one-to-one. Thus, we can equate the arguments of the cosecant function:
$90^\circ - 4A = A – 20^\circ$
Now, we solve this linear equation for A.
Add $4A$ to both sides:
$90^\circ = A – 20^\circ + 4A$
$90^\circ = 5A – 20^\circ$
Add $20^\circ$ to both sides:
$90^\circ + 20^\circ = 5A$
$110^\circ = 5A$
Divide by 5:
$A = \frac{110^\circ}{5}$
$A = 22^\circ$
Let's verify the condition that 4A is an acute angle:
$4A = 4 \times 22^\circ = 88^\circ$. Since $0^\circ < 88^\circ < 90^\circ$, 4A is indeed an acute angle.
Also, $A - 20^\circ = 22^\circ - 20^\circ = 2^\circ$, which is positive.
The value of A is $22^\circ$.
Question 6. If A, B and C are interior angles of a triangle ABC, then show that
sin $\left( \frac{B \;+\; C}{2} \right)$ = cos $\frac{A}{2}$
Answer:
Given:
A, B, and C are the interior angles of a triangle ABC.
To Show:
$\sin \left( \frac{B + C}{2} \right) = \cos \frac{A}{2}$
Solution:
Since A, B, and C are the interior angles of a triangle, their sum is $180^\circ$.
A + B + C = $180^\circ$
(Angle sum property of a triangle)
We need the expression $\frac{B+C}{2}$. Let's isolate B + C from the equation:
B + C = $180^\circ$ - A
Now, divide both sides of the equation by 2:
$\frac{B + C}{2} = \frac{180^\circ - A}{2}$
$\frac{B + C}{2} = \frac{180^\circ}{2} - \frac{A}{2}$
$\frac{B + C}{2} = 90^\circ - \frac{A}{2}$
Now, take the sine of both sides of this equation:
$\sin \left( \frac{B + C}{2} \right) = \sin \left( 90^\circ - \frac{A}{2} \right)$
We use the trigonometric identity for complementary angles: $\sin (90^\circ - \theta) = \cos \theta$.
Here, $\theta = \frac{A}{2}$.
So, $\sin \left( 90^\circ - \frac{A}{2} \right) = \cos \frac{A}{2}$.
Substitute this back into the equation:
$\sin \left( \frac{B + C}{2} \right) = \cos \frac{A}{2}$
This matches the required identity.
Hence Shown.
Question 7. Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Answer:
To Express:
$\sin 67^\circ + \cos 75^\circ$ in terms of trigonometric ratios of angles between $0^\circ$ and $45^\circ$.
Solution:
We need to express the given trigonometric ratios of angles $67^\circ$ and $75^\circ$ (which are greater than $45^\circ$) in terms of trigonometric ratios of angles between $0^\circ$ and $45^\circ$.
We use the complementary angle identities:
$\sin \theta = \cos (90^\circ - \theta)$
$\cos \theta = \sin (90^\circ - \theta)$
For the term $\sin 67^\circ$:
The angle is $67^\circ$. The complementary angle is $90^\circ - 67^\circ = 23^\circ$.
$\sin 67^\circ = \sin (90^\circ - 23^\circ) = \cos 23^\circ$
The angle $23^\circ$ is between $0^\circ$ and $45^\circ$.
For the term $\cos 75^\circ$:
The angle is $75^\circ$. The complementary angle is $90^\circ - 75^\circ = 15^\circ$.
$\cos 75^\circ = \cos (90^\circ - 15^\circ) = \sin 15^\circ$
The angle $15^\circ$ is between $0^\circ$ and $45^\circ$.
Now, substitute these expressions back into the original sum:
$\sin 67^\circ + \cos 75^\circ = \cos 23^\circ + \sin 15^\circ$
The expression $\sin 67^\circ + \cos 75^\circ$ is expressed in terms of trigonometric ratios of angles $23^\circ$ and $15^\circ$, both of which are between $0^\circ$ and $45^\circ$.
The expression is $\cos 23^\circ + \sin 15^\circ$.
Example 12 to 15 (Before Exercise 8.4)
Example 12. Express the ratios cos A, tan A and sec A in terms of sin A.
Answer:
Given:
Trigonometric ratios $\cos A$, $\tan A$, and $\sec A$.
To Express:
$\cos A$, $\tan A$, and $\sec A$ in terms of $\sin A$.
Solution:
We use fundamental trigonometric identities.
Expressing $\cos A$ in terms of $\sin A$:
We use the Pythagorean identity: $\sin^2 A + \cos^2 A = 1$.
Subtract $\sin^2 A$ from both sides:
$\cos^2 A = 1 - \sin^2 A$
Take the square root of both sides:
$\cos A = \pm \sqrt{1 - \sin^2 A}$
In problems involving angles in a right triangle, A is typically an acute angle ($0^\circ < A < 90^\circ$). In this range, $\cos A$ is positive. If A could be other angles, the sign would depend on the quadrant of A.
Assuming A is an acute angle:
$\cos A = \sqrt{1 - \sin^2 A}$
Expressing $\tan A$ in terms of $\sin A$:
We use the definition of tangent in terms of sine and cosine: $\tan A = \frac{\sin A}{\cos A}$.
Now substitute the expression for $\cos A$ in terms of $\sin A$ (assuming A is acute):
$\tan A = \frac{\sin A}{\sqrt{1 - \sin^2 A}}$
Expressing $\sec A$ in terms of $\sin A$:
We use the reciprocal identity: $\sec A = \frac{1}{\cos A}$.
Now substitute the expression for $\cos A$ in terms of $\sin A$ (assuming A is acute):
$\sec A = \frac{1}{\sqrt{1 - \sin^2 A}}$
Summary of the expressions in terms of $\sin A$ (assuming A is an acute angle):
$\cos A = \sqrt{1 - \sin^2 A}$
$\tan A = \frac{\sin A}{\sqrt{1 - \sin^2 A}}$
$\sec A = \frac{1}{\sqrt{1 - \sin^2 A}}$
Example 13. Prove that sec A (1 – sin A)(sec A + tan A) = 1.
Answer:
Given:
The identity $\sec A (1 – \sin A)(\sec A + \tan A) = 1$.
To Prove:
$\sec A (1 – \sin A)(\sec A + \tan A) = 1$
Proof:
Consider the Left Hand Side (LHS) of the identity:
LHS = $\sec A (1 – \sin A)(\sec A + \tan A)$
Express $\sec A$ and $\tan A$ in terms of $\sin A$ and $\cos A$ using the identities $\sec A = \frac{1}{\cos A}$ and $\tan A = \frac{\sin A}{\cos A}$.
Substitute these into the LHS:
LHS = $\frac{1}{\cos A} (1 – \sin A)\left(\frac{1}{\cos A} + \frac{\sin A}{\cos A}\right)$
Combine the terms within the second parenthesis:
LHS = $\frac{1}{\cos A} (1 – \sin A)\left(\frac{1 + \sin A}{\cos A}\right)$
Multiply the terms in the expression:
LHS = $\frac{1 \times (1 – \sin A) \times (1 + \sin A)}{\cos A \times \cos A}$
LHS = $\frac{(1 – \sin A)(1 + \sin A)}{\cos^2 A}$
Apply the algebraic identity $(a-b)(a+b) = a^2 - b^2$ to the numerator:
LHS = $\frac{1^2 – \sin^2 A}{\cos^2 A}$
LHS = $\frac{1 – \sin^2 A}{\cos^2 A}$
Use the fundamental trigonometric identity $\sin^2 A + \cos^2 A = 1$, which implies $1 – \sin^2 A = \cos^2 A$.
Substitute $1 – \sin^2 A$ with $\cos^2 A$ in the numerator:
LHS = $\frac{\cos^2 A}{\cos^2 A}$
Assuming $\cos^2 A \neq 0$ (which is true for values of A where $\sec A$ and $\tan A$ are defined, i.e., $A \neq 90^\circ, 270^\circ, ...$), we can cancel the $\cos^2 A$ terms:
LHS = 1
This is equal to the Right Hand Side (RHS).
LHS = RHS
Hence Proved.
Example 14. Prove that $\frac{cot \;A \;-\; cos \;A}{cot \;A \;+\; cos\; A}$ = $\frac{cosec \;A \;-\; 1}{cosec \;A \;+\; 1}$
Answer:
Given:
The identity $\frac{\cot A – \cos A}{\cot A + \cos A} = \frac{\text{cosec } A – 1}{\text{cosec } A + 1}$.
To Prove:
$\frac{\cot A – \cos A}{\cot A + \cos A} = \frac{\text{cosec } A – 1}{\text{cosec } A + 1}$
Proof:
Consider the Left Hand Side (LHS) of the identity:
LHS = $\frac{\cot A – \cos A}{\cot A + \cos A}$
Express $\cot A$ in terms of $\sin A$ and $\cos A$ using the identity $\cot A = \frac{\cos A}{\sin A}$.
Substitute this into the LHS:
LHS = $\frac{\frac{\cos A}{\sin A} – \cos A}{\frac{\cos A}{\sin A} + \cos A}$
Factor out $\cos A$ from the numerator and the denominator:
LHS = $\frac{\cos A \left(\frac{1}{\sin A} – 1\right)}{\cos A \left(\frac{1}{\sin A} + 1\right)}$
Assuming $\cos A \neq 0$, we can cancel the $\cos A$ terms:
LHS = $\frac{\frac{1}{\sin A} – 1}{\frac{1}{\sin A} + 1}$
We know that $\frac{1}{\sin A} = \text{cosec } A$.
Substitute this into the expression:
LHS = $\frac{\text{cosec } A – 1}{\text{cosec } A + 1}$
This is equal to the Right Hand Side (RHS).
LHS = RHS
Hence Proved.
Alternate Proof (Starting from RHS):
Consider the Right Hand Side (RHS) of the identity:
RHS = $\frac{\text{cosec } A – 1}{\text{cosec } A + 1}$
Express $\text{cosec } A$ in terms of $\sin A$ using the identity $\text{cosec } A = \frac{1}{\sin A}$.
Substitute this into the RHS:
RHS = $\frac{\frac{1}{\sin A} – 1}{\frac{1}{\sin A} + 1}$
Multiply the numerator and the denominator by $\sin A$ to clear the fractions:
RHS = $\frac{\left(\frac{1}{\sin A} – 1\right) \times \sin A}{\left(\frac{1}{\sin A} + 1\right) \times \sin A}$
RHS = $\frac{1 – \sin A}{\sin A} \times \frac{\sin A}{1 + \sin A}$
No, that's not correct. It should be distributing the $\sin A$ in numerator and denominator.
RHS = $\frac{\frac{1}{\sin A} \times \sin A – 1 \times \sin A}{\frac{1}{\sin A} \times \sin A + 1 \times \sin A}$
RHS = $\frac{1 – \sin A}{1 + \sin A}$
Now, relate this back to the LHS. This expression $(1-\sin A)/(1+\sin A)$ is not immediately the form of the LHS. Let's go back to the step where we had the LHS in terms of $\sin A$ and $\cos A$.
LHS = $\frac{\frac{\cos A}{\sin A} – \cos A}{\frac{\cos A}{\sin A} + \cos A}$
Multiply the numerator and denominator by $\sin A$:
LHS = $\frac{(\frac{\cos A}{\sin A} – \cos A) \times \sin A}{(\frac{\cos A}{\sin A} + \cos A) \times \sin A}$
LHS = $\frac{\frac{\cos A}{\sin A} \times \sin A – \cos A \times \sin A}{\frac{\cos A}{\sin A} \times \sin A + \cos A \times \sin A}$
LHS = $\frac{\cos A – \cos A \sin A}{\cos A + \cos A \sin A}$
Factor out $\cos A$ from the numerator and denominator:
LHS = $\frac{\cos A (1 – \sin A)}{\cos A (1 + \sin A)}$
Assuming $\cos A \neq 0$, we can cancel $\cos A$:
LHS = $\frac{1 – \sin A}{1 + \sin A}$
Now consider the RHS again:
RHS = $\frac{\text{cosec } A – 1}{\text{cosec } A + 1}$
Substitute $\text{cosec } A = \frac{1}{\sin A}$:
RHS = $\frac{\frac{1}{\sin A} – 1}{\frac{1}{\sin A} + 1}$
Find a common denominator in the numerator and denominator:
RHS = $\frac{\frac{1 - \sin A}{\sin A}}{\frac{1 + \sin A}{\sin A}}$
Invert the denominator and multiply:
RHS = $\frac{1 - \sin A}{\sin A} \times \frac{\sin A}{1 + \sin A}$
Assuming $\sin A \neq 0$, we can cancel $\sin A$:
RHS = $\frac{1 - \sin A}{1 + \sin A}$
Since LHS = $\frac{1 - \sin A}{1 + \sin A}$ and RHS = $\frac{1 - \sin A}{1 + \sin A}$, we have LHS = RHS.
Hence Proved.
The first proof (starting from LHS and converting to $\sin A$ and $\cos A$) was more direct and simpler.
Example 15. Prove that $\frac{sin \;θ \;-\; cos \;θ \;+\; 1}{sin \;θ \;+\; cos \;θ \;-\; 1}$ = $\frac{1}{sec \;θ \;-\; tan \;θ}$ , using the identity sec2 θ = 1 + tan2 θ.
Answer:
Given:
The identity $\frac{\sin \theta – \cos \theta + 1}{\sin \theta + \cos \theta – 1} = \frac{1}{\sec \theta – \tan \theta}$.
The identity $\sec^2 \theta = 1 + \tan^2 \theta$ is to be used.
To Prove:
$\frac{\sin \theta – \cos \theta + 1}{\sin \theta + \cos \theta – 1} = \frac{1}{\sec \theta – \tan \theta}$
Proof:
Consider the Left Hand Side (LHS) of the identity:
LHS = $\frac{\sin \theta – \cos \theta + 1}{\sin \theta + \cos \theta – 1}$
To express the terms in $\tan \theta$ and $\sec \theta$, divide the numerator and the denominator by $\cos \theta$, assuming $\cos \theta \neq 0$.
LHS = $\frac{\frac{\sin \theta}{\cos \theta} – \frac{\cos \theta}{\cos \theta} + \frac{1}{\cos \theta}}{\frac{\sin \theta}{\cos \theta} + \frac{\cos \theta}{\cos \theta} – \frac{1}{\cos \theta}}$
Using the identities $\tan \theta = \frac{\sin \theta}{\cos \theta}$ and $\sec \theta = \frac{1}{\cos \theta}$:
LHS = $\frac{\tan \theta – 1 + \sec \theta}{\tan \theta + 1 – \sec \theta}$
Rearrange the terms in the numerator:
LHS = $\frac{\tan \theta + \sec \theta – 1}{\tan \theta – \sec \theta + 1}$
We are asked to use the identity $\sec^2 \theta = 1 + \tan^2 \theta$. This identity can be rearranged to $1 = \sec^2 \theta - \tan^2 \theta$.
Using the difference of squares formula, $a^2 - b^2 = (a-b)(a+b)$, we have $\sec^2 \theta - \tan^2 \theta = (\sec \theta - \tan \theta)(\sec \theta + \tan \theta)$.
So, $1 = (\sec \theta - \tan \theta)(\sec \theta + \tan \theta)$.
Substitute this expression for '1' into the numerator of the LHS:
Numerator = $(\tan \theta + \sec \theta) – 1$
Numerator = $(\tan \theta + \sec \theta) – (\sec^2 \theta - \tan^2 \theta)$
Numerator = $(\tan \theta + \sec \theta) – (\sec \theta - \tan \theta)(\sec \theta + \tan \theta)$
Now, factor out the common term $(\tan \theta + \sec \theta)$ from the numerator:
Numerator = $(\tan \theta + \sec \theta) [1 – (\sec \theta - \tan \theta)]$
Numerator = $(\tan \theta + \sec \theta) [1 – \sec \theta + \tan \theta]$
Numerator = $(\tan \theta + \sec \theta) [\tan \theta – \sec \theta + 1]$
Substitute this back into the LHS expression:
LHS = $\frac{(\tan \theta + \sec \theta) (\tan \theta – \sec \theta + 1)}{\tan \theta – \sec \theta + 1}$
Assuming $\tan \theta – \sec \theta + 1 \neq 0$, we can cancel the common factor from the numerator and the denominator:
LHS = $\tan \theta + \sec \theta$
Now, consider the Right Hand Side (RHS) of the identity:
RHS = $\frac{1}{\sec \theta – \tan \theta}$
To simplify the RHS and relate it to the LHS result, multiply the numerator and denominator by the conjugate of the denominator, which is $\sec \theta + \tan \theta$, assuming $\sec \theta - \tan \theta \neq 0$ and $\sec \theta + \tan \theta \neq 0$.
RHS = $\frac{1}{\sec \theta – \tan \theta} \times \frac{\sec \theta + \tan \theta}{\sec \theta + \tan \theta}$
RHS = $\frac{\sec \theta + \tan \theta}{(\sec \theta – \tan \theta)(\sec \theta + \tan \theta)}$
Apply the difference of squares formula in the denominator:
RHS = $\frac{\sec \theta + \tan \theta}{\sec^2 \theta – \tan^2 \theta}$
Using the given identity $\sec^2 \theta = 1 + \tan^2 \theta$, we have $\sec^2 \theta – \tan^2 \theta = 1$.
Substitute this into the denominator of the RHS:
RHS = $\frac{\sec \theta + \tan \theta}{1}$
RHS = $\sec \theta + \tan \theta$
Since LHS = $\sec \theta + \tan \theta$ and RHS = $\sec \theta + \tan \theta$, we have:
LHS = RHS
The identity is proven for all values of $\theta$ for which $\cos \theta \neq 0$ (so $\tan \theta$ and $\sec \theta$ are defined) and the denominators in the original expression and during simplification are non-zero.
Hence Proved.
Exercise 8.4
Question 1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Answer:
Given:
Trigonometric ratios $\sin A$, $\sec A$, and $\tan A$.
To Express:
$\sin A$, $\sec A$, and $\tan A$ in terms of $\cot A$.
Solution:
We use fundamental trigonometric identities.
Expressing $\tan A$ in terms of $\cot A$:
We use the reciprocal identity: $\tan A = \frac{1}{\cot A}$.
Expressing $\sin A$ in terms of $\cot A$:
We use the identity $\text{cosec}^2 A = 1 + \cot^2 A$.
Taking the square root of both sides:
$\text{cosec } A = \pm \sqrt{1 + \cot^2 A}$
In this chapter, we usually consider acute angles, where trigonometric ratios are positive. So, assuming A is an acute angle:
$\text{cosec } A = \sqrt{1 + \cot^2 A}$
We also know the reciprocal identity $\sin A = \frac{1}{\text{cosec } A}$.
Substitute the expression for $\text{cosec } A$:
$\sin A = \frac{1}{\sqrt{1 + \cot^2 A}}$
Expressing $\sec A$ in terms of $\cot A$:
We use the identity $\sec^2 A = 1 + \tan^2 A$.
We already expressed $\tan A$ in terms of $\cot A$: $\tan A = \frac{1}{\cot A}$.
Substitute this into the identity for $\sec^2 A$:
$\sec^2 A = 1 + \left(\frac{1}{\cot A}\right)^2$
$\sec^2 A = 1 + \frac{1}{\cot^2 A}$
Find a common denominator on the right side:
$\sec^2 A = \frac{\cot^2 A + 1}{\cot^2 A}$
Taking the square root of both sides, and assuming A is acute (so $\sec A > 0$):
$\sec A = \sqrt{\frac{\cot^2 A + 1}{\cot^2 A}}$
$\sec A = \frac{\sqrt{1 + \cot^2 A}}{\sqrt{\cot^2 A}}$
$\sec A = \frac{\sqrt{1 + \cot^2 A}}{|\cot A|}$
For an acute angle A, $\cot A$ is positive, so $|\cot A| = \cot A$.
$\sec A = \frac{\sqrt{1 + \cot^2 A}}{\cot A}$
Summary of the expressions in terms of $\cot A$ (assuming A is an acute angle):
$\sin A = \frac{1}{\sqrt{1 + \cot^2 A}}$
$\sec A = \frac{\sqrt{1 + \cot^2 A}}{\cot A}$
$\tan A = \frac{1}{\cot A}$
Question 2. Write all the other trigonometric ratios of ∠ A in terms of sec A.
Answer:
Given:
Angle A.
To Express:
All other trigonometric ratios of $\angle$ A ($\sin A$, $\cos A$, $\tan A$, $\text{cosec } A$, $\cot A$) in terms of $\sec A$.
Solution:
We use fundamental trigonometric identities to express each ratio in terms of $\sec A$. We assume that A is an acute angle, which is standard in this context, unless otherwise specified. For acute angles, all trigonometric ratios are positive, allowing us to take the positive square root.
1. Express $\cos A$ in terms of $\sec A$:
We use the reciprocal identity:
$\cos A = \frac{1}{\sec A}$
2. Express $\tan A$ in terms of $\sec A$:
We use the identity $\sec^2 A = 1 + \tan^2 A$.
Rearrange the identity to solve for $\tan^2 A$:
$\tan^2 A = \sec^2 A - 1$
Take the square root of both sides. For acute angle A, $\tan A$ is positive, so we take the positive root:
$\tan A = \sqrt{\sec^2 A - 1}$
3. Express $\sin A$ in terms of $\sec A$:
We use the identity $\sin^2 A + \cos^2 A = 1$.
Rearrange the identity to solve for $\sin^2 A$:
$\sin^2 A = 1 - \cos^2 A$
Substitute the expression for $\cos A$ in terms of $\sec A$ ($\cos A = \frac{1}{\sec A}$):
$\sin^2 A = 1 - \left(\frac{1}{\sec A}\right)^2 = 1 - \frac{1}{\sec^2 A}$
Find a common denominator on the right side:
$\sin^2 A = \frac{\sec^2 A - 1}{\sec^2 A}$
Take the square root of both sides. For acute angle A, $\sin A$ is positive, so we take the positive root:
$\sin A = \sqrt{\frac{\sec^2 A - 1}{\sec^2 A}} = \frac{\sqrt{\sec^2 A - 1}}{\sqrt{\sec^2 A}} = \frac{\sqrt{\sec^2 A - 1}}{|\sec A|}$
For acute angle A, $\sec A$ is positive, so $|\sec A| = \sec A$:
$\sin A = \frac{\sqrt{\sec^2 A - 1}}{\sec A}$
4. Express $\text{cosec } A$ in terms of $\sec A$:
We use the reciprocal identity $\text{cosec } A = \frac{1}{\sin A}$.
Substitute the expression for $\sin A$ in terms of $\sec A$:
$\text{cosec } A = \frac{1}{\frac{\sqrt{\sec^2 A - 1}}{\sec A}}$
$\text{cosec } A = \frac{\sec A}{\sqrt{\sec^2 A - 1}}$
5. Express $\cot A$ in terms of $\sec A$:
We use the reciprocal identity $\cot A = \frac{1}{\tan A}$.
Substitute the expression for $\tan A$ in terms of $\sec A$ (assuming $\tan A > 0$):
$\cot A = \frac{1}{\sqrt{\sec^2 A - 1}}$
The other trigonometric ratios of $\angle$ A in terms of $\sec A$ (for acute angle A) are:
$\sin A = \frac{\sqrt{\sec^2 A - 1}}{\sec A}$
$\cos A = \frac{1}{\sec A}$
$\tan A = \sqrt{\sec^2 A - 1}$
$\text{cosec } A = \frac{\sec A}{\sqrt{\sec^2 A - 1}}$
$\cot A = \frac{1}{\sqrt{\sec^2 A - 1}}$
Question 3. Evaluate :
(i) $\frac{sin^2 \;63° \;+\; sin^2 \;27°}{cos^2 \;17° \;+\; cos^2 \;73°}$
(ii) sin 25° cos 65° + cos 25° sin 65°
Answer:
(i) Evaluate $\frac{\sin^2 63^\circ + \sin^2 27^\circ}{\cos^2 17^\circ + \cos^2 73^\circ}$:
Consider the numerator: $\sin^2 63^\circ + \sin^2 27^\circ$.
Notice that $63^\circ + 27^\circ = 90^\circ$. These are complementary angles.
We use the identity $\sin (90^\circ - \theta) = \cos \theta$ or $\cos (90^\circ - \theta) = \sin \theta$.
We can write $\sin 63^\circ = \sin (90^\circ - 27^\circ) = \cos 27^\circ$.
So, $\sin^2 63^\circ = (\sin 63^\circ)^2 = (\cos 27^\circ)^2 = \cos^2 27^\circ$.
Numerator = $\cos^2 27^\circ + \sin^2 27^\circ$.
Using the identity $\sin^2 \theta + \cos^2 \theta = 1$, with $\theta = 27^\circ$, we get:
Numerator = 1.
Consider the denominator: $\cos^2 17^\circ + \cos^2 73^\circ$.
Notice that $17^\circ + 73^\circ = 90^\circ$. These are complementary angles.
We can write $\cos 73^\circ = \cos (90^\circ - 17^\circ) = \sin 17^\circ$.
So, $\cos^2 73^\circ = (\cos 73^\circ)^2 = (\sin 17^\circ)^2 = \sin^2 17^\circ$.
Denominator = $\cos^2 17^\circ + \sin^2 17^\circ$.
Using the identity $\sin^2 \theta + \cos^2 \theta = 1$, with $\theta = 17^\circ$, we get:
Denominator = 1.
Now, evaluate the entire expression:
$\frac{\sin^2 63^\circ + \sin^2 27^\circ}{\cos^2 17^\circ + \cos^2 73^\circ} = \frac{1}{1} = 1$
The value is 1.
(ii) Evaluate $\sin 25^\circ \cos 65^\circ + \cos 25^\circ \sin 65^\circ$:
Notice that $25^\circ + 65^\circ = 90^\circ$. These are complementary angles.
We use the identity $\sin (90^\circ - \theta) = \cos \theta$ and $\cos (90^\circ - \theta) = \sin \theta$.
We can write $\cos 65^\circ = \cos (90^\circ - 25^\circ) = \sin 25^\circ$.
We can write $\sin 65^\circ = \sin (90^\circ - 25^\circ) = \cos 25^\circ$.
Substitute these into the expression:
$\sin 25^\circ \cos 65^\circ + \cos 25^\circ \sin 65^\circ = \sin 25^\circ (\sin 25^\circ) + \cos 25^\circ (\cos 25^\circ)$
$= \sin^2 25^\circ + \cos^2 25^\circ$
Using the identity $\sin^2 \theta + \cos^2 \theta = 1$, with $\theta = 25^\circ$, we get:
$= 1$
Alternatively, using angle sum identity:
Recall the sine addition formula: $\sin (A + B) = \sin A \cos B + \cos A \sin B$.
The expression $\sin 25^\circ \cos 65^\circ + \cos 25^\circ \sin 65^\circ$ matches the form of $\sin (A + B)$ with $A = 25^\circ$ and $B = 65^\circ$.
$\sin 25^\circ \cos 65^\circ + \cos 25^\circ \sin 65^\circ = \sin (25^\circ + 65^\circ)$
$= \sin 90^\circ$
We know that $\sin 90^\circ = 1$.
The value is 1.
Question 4. Choose the correct option. Justify your choice.
(i) 9 sec2 A – 9 tan2 A =
(A) 1
(B) 9
(C) 8
(D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =
(A) 0
(B) 1
(C) 2
(D) –1
(iii) (sec A + tan A) (1 – sin A) =
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
(iv) $\frac{1 \;+\; tan^2 \;A}{1 \;+\; cot^2 \;A}$ =
(A) sec2 A
(B) –1
(C) cot2 A
(D) tan2 A
Answer:
(i) Evaluate $9 \sec^2 A – 9 \tan^2 A$:
Given expression: $9 \sec^2 A – 9 \tan^2 A$
Factor out the common factor 9:
$= 9 (\sec^2 A – \tan^2 A)$
We use the trigonometric identity $\sec^2 A = 1 + \tan^2 A$.
Rearrange the identity: $\sec^2 A – \tan^2 A = 1$.
Substitute this into the expression:
$= 9 (1)$
$= 9$
The value of the expression is 9.
Comparing with the options, the correct option is (B).
The correct option is (B).
Justification: By factoring and using the identity $\sec^2 A – \tan^2 A = 1$, the expression simplifies to 9.
(ii) Evaluate $(1 + \tan \theta + \sec \theta)(1 + \cot \theta – \text{cosec } \theta)$:
Given expression: $(1 + \tan \theta + \sec \theta)(1 + \cot \theta – \text{cosec } \theta)$
Express $\tan \theta$, $\sec \theta$, $\cot \theta$, and $\text{cosec } \theta$ in terms of $\sin \theta$ and $\cos \theta$:
$\tan \theta = \frac{\sin \theta}{\cos \theta}$, $\sec \theta = \frac{1}{\cos \theta}$, $\cot \theta = \frac{\cos \theta}{\sin \theta}$, $\text{cosec } \theta = \frac{1}{\sin \theta}$.
Substitute these into the expression:
$(1 + \frac{\sin \theta}{\cos \theta} + \frac{1}{\cos \theta})(1 + \frac{\cos \theta}{\sin \theta} – \frac{1}{\sin \theta})$
Find a common denominator within each parenthesis:
$\left(\frac{\cos \theta}{\cos \theta} + \frac{\sin \theta}{\cos \theta} + \frac{1}{\cos \theta}\right)\left(\frac{\sin \theta}{\sin \theta} + \frac{\cos \theta}{\sin \theta} – \frac{1}{\sin \theta}\right)$
$\left(\frac{\cos \theta + \sin \theta + 1}{\cos \theta}\right)\left(\frac{\sin \theta + \cos \theta – 1}{\sin \theta}\right)$
Multiply the two fractions:
$\frac{(\cos \theta + \sin \theta + 1)(\sin \theta + \cos \theta – 1)}{\cos \theta \sin \theta}$
In the numerator, group $(\cos \theta + \sin \theta)$ together. The numerator is in the form $(a+b)(a-b)$ where $a = (\cos \theta + \sin \theta)$ and $b = 1$.
Numerator = $((\cos \theta + \sin \theta) + 1)((\cos \theta + \sin \theta) – 1)$
Numerator = $(\cos \theta + \sin \theta)^2 - 1^2$
Expand $(\cos \theta + \sin \theta)^2$ using $(a+b)^2 = a^2 + 2ab + b^2$:
Numerator = $(\cos^2 \theta + 2 \cos \theta \sin \theta + \sin^2 \theta) - 1$
Use the identity $\sin^2 \theta + \cos^2 \theta = 1$:
Numerator = $(1 + 2 \cos \theta \sin \theta) - 1$
Numerator = $1 + 2 \cos \theta \sin \theta - 1 = 2 \cos \theta \sin \theta$
Substitute the numerator back into the expression:
$\frac{2 \cos \theta \sin \theta}{\cos \theta \sin \theta}$
Assuming $\cos \theta \sin \theta \neq 0$, cancel the common term:
$= 2$
The value of the expression is 2.
Comparing with the options, the correct option is (C).
The correct option is (C).
Justification: By converting the terms to $\sin \theta$ and $\cos \theta$ and simplifying using algebraic and trigonometric identities, the expression evaluates to 2.
(iii) Evaluate $(\sec A + \tan A)(1 – \sin A)$:
Given expression: $(\sec A + \tan A)(1 – \sin A)$
Express $\sec A$ and $\tan A$ in terms of $\sin A$ and $\cos A$:
$\sec A = \frac{1}{\cos A}$, $\tan A = \frac{\sin A}{\cos A}$.
Substitute these into the first parenthesis:
$\left(\frac{1}{\cos A} + \frac{\sin A}{\cos A}\right)(1 – \sin A)$
Combine the terms within the first parenthesis:
$\left(\frac{1 + \sin A}{\cos A}\right)(1 – \sin A)$
Multiply the terms:
$\frac{(1 + \sin A)(1 – \sin A)}{\cos A}$
Apply the algebraic identity $(a+b)(a-b) = a^2 - b^2$ to the numerator:
$\frac{1^2 – \sin^2 A}{\cos A} = \frac{1 – \sin^2 A}{\cos A}$
Use the fundamental trigonometric identity $\sin^2 A + \cos^2 A = 1$, which implies $1 – \sin^2 A = \cos^2 A$.
Substitute $1 – \sin^2 A$ with $\cos^2 A$ in the numerator:
$\frac{\cos^2 A}{\cos A}$
Assuming $\cos A \neq 0$, we can cancel one power of $\cos A$:
$\cos A$
The value of the expression is $\cos A$.
Comparing with the options, the correct option is (D).
The correct option is (D).
Justification: By converting the terms to $\sin A$ and $\cos A$ and simplifying using algebraic and trigonometric identities, the expression evaluates to $\cos A$.
(iv) Evaluate $\frac{1 + \tan^2 A}{1 + \cot^2 A}$:
Given expression: $\frac{1 + \tan^2 A}{1 + \cot^2 A}$
We use the trigonometric identities $\sec^2 A = 1 + \tan^2 A$ and $\text{cosec}^2 A = 1 + \cot^2 A$.
Substitute these into the numerator and denominator:
$\frac{\sec^2 A}{\text{cosec}^2 A}$
Express $\sec^2 A$ and $\text{cosec}^2 A$ in terms of $\sin A$ and $\cos A$:
$\sec^2 A = \left(\frac{1}{\cos A}\right)^2 = \frac{1}{\cos^2 A}$
$\text{cosec}^2 A = \left(\frac{1}{\sin A}\right)^2 = \frac{1}{\sin^2 A}$
Substitute these back into the expression:
$\frac{\frac{1}{\cos^2 A}}{\frac{1}{\sin^2 A}}$
Invert the denominator and multiply:
$\frac{1}{\cos^2 A} \times \frac{\sin^2 A}{1}$
$= \frac{\sin^2 A}{\cos^2 A}$
We know that $\frac{\sin A}{\cos A} = \tan A$. Therefore, $\frac{\sin^2 A}{\cos^2 A} = \left(\frac{\sin A}{\cos A}\right)^2 = \tan^2 A$.
The value of the expression is $\tan^2 A$.
Comparing with the options, the correct option is (D).
The correct option is (D).
Justification: By using the identities $1 + \tan^2 A = \sec^2 A$ and $1 + \cot^2 A = \text{cosec}^2 A$, and then converting to $\sin A$ and $\cos A$, the expression simplifies to $\tan^2 A$.
Question 5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
(i) (cosec θ - cot θ)2 = $\frac{1 \;-\; cos \;θ}{ 1 \;+\; cos \;θ}$
(ii) $\frac{cos \;A}{1 \;+\; sin \;A}$ + $\frac{1 \;+\; sin \;A}{cos \;A}$ = 2 sec A
(iii) $\frac{tan \;θ}{1 \;-\; cot \;θ}$ + $\frac{cot \;θ}{1 \;-\; tan \;θ}$ = 1 + sec θ cosec θ
[Hint: Write the expression in terms of sin θ and cos θ]
(iv) $\frac{1 \;+\; sec \;A}{sec \;A}$ = $\frac{sin^2 \;A}{1 \;-\; cos \;A}$
[Hint: Simplify LHS and RHS separately]
(v) $\frac{cos \;A \;-\; sin \;A \;+\; 1}{cos \;A \;+\; sin \;A \;-\; 1}$ = cosec A + cot A, using the identity cosec2 A = 1 + cot2 A.
(vi) $\sqrt{\frac{1 \;+\; sin \;A}{1 \;-\; sin \;A}}$ = sec A + tan A
(vii) $\frac{sin \;θ \;-\; 2sin^3 \;θ}{2 cos^3 \;θ \;-\; cos \;θ}$ = tan θ
(viii) (sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2 A + cot2 A
(ix) (cosec A – sin A)(sec A – cos A) = $\frac{1}{tan \;A \;+\; cot \;A}$
[Hint: Simplify LHS and RHS separately]
(x) $\left( \frac{1\;+\;tan^{2}\;A}{1\;+\;cot^{2}\;A} \right)$ = $\left(\frac{1\;-\;tan \;A}{1\;-\;cot \;A} \right)^{2}$ = tan2 A
Answer:
(i) Prove that $(\text{cosec } \theta - \cot \theta)^2 = \frac{1 - \cos \theta}{1 + \cos \theta}$:
Consider the Left Hand Side (LHS):
LHS = $(\text{cosec } \theta - \cot \theta)^2$
Express $\text{cosec } \theta$ and $\cot \theta$ in terms of $\sin \theta$ and $\cos \theta$:
$\text{cosec } \theta = \frac{1}{\sin \theta}$ and $\cot \theta = \frac{\cos \theta}{\sin \theta}$.
Substitute these into the LHS:
LHS = $\left(\frac{1}{\sin \theta} - \frac{\cos \theta}{\sin \theta}\right)^2$
Combine the terms inside the parenthesis:
LHS = $\left(\frac{1 - \cos \theta}{\sin \theta}\right)^2$
Square the numerator and the denominator separately:
LHS = $\frac{(1 - \cos \theta)^2}{\sin^2 \theta}$
Use the identity $\sin^2 \theta + \cos^2 \theta = 1$, which implies $\sin^2 \theta = 1 - \cos^2 \theta$.
Substitute $1 - \cos^2 \theta$ for $\sin^2 \theta$ in the denominator:
LHS = $\frac{(1 - \cos \theta)^2}{1 - \cos^2 \theta}$
Apply the difference of squares formula, $a^2 - b^2 = (a-b)(a+b)$, to the denominator, where $a=1$ and $b=\cos \theta$: $1 - \cos^2 \theta = (1 - \cos \theta)(1 + \cos \theta)$.
LHS = $\frac{(1 - \cos \theta)^2}{(1 - \cos \theta)(1 + \cos \theta)}$
Assume $1 - \cos \theta \neq 0$, which means $\cos \theta \neq 1$ (i.e., $\theta \neq 0^\circ, 360^\circ, ...$). For acute angles, this is true.
Cancel the common factor $(1 - \cos \theta)$ from the numerator and the denominator:
LHS = $\frac{1 - \cos \theta}{1 + \cos \theta}$
This is equal to the Right Hand Side (RHS).
LHS = RHS
Hence Proved.
(ii) Prove that $\frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A} = 2 \sec A$:
Consider the Left Hand Side (LHS):
LHS = $\frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A}$
Find a common denominator, which is $(1 + \sin A)(\cos A)$:
LHS = $\frac{(\cos A)(\cos A) + (1 + \sin A)(1 + \sin A)}{(1 + \sin A)(\cos A)}$
LHS = $\frac{\cos^2 A + (1 + \sin A)^2}{(1 + \sin A)(\cos A)}$
Expand $(1 + \sin A)^2$ using $(a+b)^2 = a^2 + 2ab + b^2$:
LHS = $\frac{\cos^2 A + (1^2 + 2(1)(\sin A) + \sin^2 A)}{(1 + \sin A)(\cos A)}$
LHS = $\frac{\cos^2 A + 1 + 2 \sin A + \sin^2 A}{(1 + \sin A)(\cos A)}$
Rearrange the terms in the numerator and use the identity $\sin^2 A + \cos^2 A = 1$:
LHS = $\frac{(\cos^2 A + \sin^2 A) + 1 + 2 \sin A}{(1 + \sin A)(\cos A)}$
LHS = $\frac{1 + 1 + 2 \sin A}{(1 + \sin A)(\cos A)}$
LHS = $\frac{2 + 2 \sin A}{(1 + \sin A)(\cos A)}$
Factor out 2 from the numerator:
LHS = $\frac{2(1 + \sin A)}{(1 + \sin A)(\cos A)}$
Assume $1 + \sin A \neq 0$ and $\cos A \neq 0$. For acute angles, this is true.
Cancel the common factor $(1 + \sin A)$ from the numerator and the denominator:
LHS = $\frac{2}{\cos A}$
Use the reciprocal identity $\sec A = \frac{1}{\cos A}$:
LHS = $2 \times \frac{1}{\cos A} = 2 \sec A$
This is equal to the Right Hand Side (RHS).
LHS = RHS
Hence Proved.
(iii) Prove that $\frac{\tan \theta}{1 - \cot \theta} + \frac{\cot \theta}{1 - \tan \theta} = 1 + \sec \theta \text{ cosec } \theta$:
Consider the Left Hand Side (LHS):
LHS = $\frac{\tan \theta}{1 - \cot \theta} + \frac{\cot \theta}{1 - \tan \theta}$
As hinted, write the expression in terms of $\sin \theta$ and $\cos \theta$.
$\tan \theta = \frac{\sin \theta}{\cos \theta}$ and $\cot \theta = \frac{\cos \theta}{\sin \theta}$.
Substitute these into the LHS:
LHS = $\frac{\frac{\sin \theta}{\cos \theta}}{1 - \frac{\cos \theta}{\sin \theta}} + \frac{\frac{\cos \theta}{\sin \theta}}{1 - \frac{\sin \theta}{\cos \theta}}$
Simplify the denominators by finding a common denominator:
$1 - \frac{\cos \theta}{\sin \theta} = \frac{\sin \theta - \cos \theta}{\sin \theta}$
$1 - \frac{\sin \theta}{\cos \theta} = \frac{\cos \theta - \sin \theta}{\cos \theta}$
Substitute these back into the LHS:
LHS = $\frac{\frac{\sin \theta}{\cos \theta}}{\frac{\sin \theta - \cos \theta}{\sin \theta}} + \frac{\frac{\cos \theta}{\sin \theta}}{\frac{\cos \theta - \sin \theta}{\cos \theta}}$
Invert the denominators and multiply:
LHS = $\frac{\sin \theta}{\cos \theta} \times \frac{\sin \theta}{\sin \theta - \cos \theta} + \frac{\cos \theta}{\sin \theta} \times \frac{\cos \theta}{\cos \theta - \sin \theta}$
LHS = $\frac{\sin^2 \theta}{\cos \theta (\sin \theta - \cos \theta)} + \frac{\cos^2 \theta}{\sin \theta (\cos \theta - \sin \theta)}$
Notice that $(\cos \theta - \sin \theta) = - (\sin \theta - \cos \theta)$. Factor out -1 from the denominator of the second term:
LHS = $\frac{\sin^2 \theta}{\cos \theta (\sin \theta - \cos \theta)} + \frac{\cos^2 \theta}{\sin \theta [- (\sin \theta - \cos \theta)]}$
LHS = $\frac{\sin^2 \theta}{\cos \theta (\sin \theta - \cos \theta)} - \frac{\cos^2 \theta}{\sin \theta (\sin \theta - \cos \theta)}$
Now the denominators are $\cos \theta (\sin \theta - \cos \theta)$ and $\sin \theta (\sin \theta - \cos \theta)$. The common denominator is $\sin \theta \cos \theta (\sin \theta - \cos \theta)$.
LHS = $\frac{\sin^2 \theta \times \sin \theta - \cos^2 \theta \times \cos \theta}{\sin \theta \cos \theta (\sin \theta - \cos \theta)}$
LHS = $\frac{\sin^3 \theta - \cos^3 \theta}{\sin \theta \cos \theta (\sin \theta - \cos \theta)}$
Apply the difference of cubes formula to the numerator: $a^3 - b^3 = (a - b)(a^2 + ab + b^2)$, where $a = \sin \theta$ and $b = \cos \theta$.
Numerator = $(\sin \theta - \cos \theta)(\sin^2 \theta + \sin \theta \cos \theta + \cos^2 \theta)$
Use the identity $\sin^2 \theta + \cos^2 \theta = 1$ in the numerator:
Numerator = $(\sin \theta - \cos \theta)(1 + \sin \theta \cos \theta)$
Substitute the numerator back into the LHS expression:
LHS = $\frac{(\sin \theta - \cos \theta)(1 + \sin \theta \cos \theta)}{\sin \theta \cos \theta (\sin \theta - \cos \theta)}$
Assume $\sin \theta - \cos \theta \neq 0$ (i.e., $\tan \theta \neq 1$, $\theta \neq 45^\circ$, etc.). For acute angles in general, this is true.
Cancel the common factor $(\sin \theta - \cos \theta)$ from the numerator and the denominator:
LHS = $\frac{1 + \sin \theta \cos \theta}{\sin \theta \cos \theta}$
Split the fraction into two terms:
LHS = $\frac{1}{\sin \theta \cos \theta} + \frac{\sin \theta \cos \theta}{\sin \theta \cos \theta}$
Use the reciprocal identities $\frac{1}{\sin \theta} = \text{cosec } \theta$ and $\frac{1}{\cos \theta} = \sec \theta$. The second term simplifies to 1.
LHS = $\text{cosec } \theta \sec \theta + 1$
Rearrange the terms:
LHS = $1 + \sec \theta \text{ cosec } \theta$
This is equal to the Right Hand Side (RHS).
LHS = RHS
Hence Proved.
(iv) Prove that $\frac{1 + \sec A}{\sec A} = \frac{\sin^2 A}{1 - \cos A}$:
As hinted, simplify LHS and RHS separately.
Consider the Left Hand Side (LHS):
LHS = $\frac{1 + \sec A}{\sec A}$
Split the fraction:
LHS = $\frac{1}{\sec A} + \frac{\sec A}{\sec A}$
Use the reciprocal identity $\cos A = \frac{1}{\sec A}$. The second term simplifies to 1.
LHS = $\cos A + 1$
Rearrange:
LHS = $1 + \cos A$
Now, consider the Right Hand Side (RHS):
RHS = $\frac{\sin^2 A}{1 - \cos A}$
Use the identity $\sin^2 A + \cos^2 A = 1$, which implies $\sin^2 A = 1 - \cos^2 A$.
Substitute $1 - \cos^2 A$ for $\sin^2 A$ in the numerator:
RHS = $\frac{1 - \cos^2 A}{1 - \cos A}$
Apply the difference of squares formula to the numerator: $a^2 - b^2 = (a-b)(a+b)$, where $a=1$ and $b=\cos A$: $1 - \cos^2 A = (1 - \cos A)(1 + \cos A)$.
RHS = $\frac{(1 - \cos A)(1 + \cos A)}{1 - \cos A}$
Assume $1 - \cos A \neq 0$, which means $\cos A \neq 1$ (i.e., $A \neq 0^\circ, 360^\circ, ...$). For acute angles, this is true unless A=0, but tan is undefined at 90, so we usually assume 0 Cancel the common factor $(1 - \cos A)$ from the numerator and the denominator: RHS = $1 + \cos A$ Since LHS = $1 + \cos A$ and RHS = $1 + \cos A$, we have: LHS = RHS Hence Proved. (v) Prove that $\frac{\cos A – \sin A + 1}{\cos A + \sin A – 1} = \text{cosec } A + \cot A$, using the identity $\text{cosec}^2 A = 1 + \cot^2 A$. Consider the Left Hand Side (LHS): LHS = $\frac{\cos A – \sin A + 1}{\cos A + \sin A – 1}$ To use the identity involving $\cot A$ and $\text{cosec } A$, divide the numerator and the denominator by $\sin A$, assuming $\sin A \neq 0$. LHS = $\frac{\frac{\cos A}{\sin A} – \frac{\sin A}{\sin A} + \frac{1}{\sin A}}{\frac{\cos A}{\sin A} + \frac{\sin A}{\sin A} – \frac{1}{\sin A}}$ Using the identities $\cot A = \frac{\cos A}{\sin A}$ and $\text{cosec } A = \frac{1}{\sin A}$: LHS = $\frac{\cot A – 1 + \text{cosec } A}{\cot A + 1 – \text{cosec } A}$ Rearrange the terms in the numerator: LHS = $\frac{\cot A + \text{cosec } A – 1}{\cot A – \text{cosec } A + 1}$ We are asked to use the identity $\text{cosec}^2 A = 1 + \cot^2 A$. This identity can be rearranged to $1 = \text{cosec}^2 A - \cot^2 A$. Using the difference of squares formula, $a^2 - b^2 = (a-b)(a+b)$, we have $\text{cosec}^2 A - \cot^2 A = (\text{cosec } A - \cot A)(\text{cosec } A + \cot A)$. So, $1 = (\text{cosec } A - \cot A)(\text{cosec } A + \cot A)$. Substitute this expression for '1' into the numerator of the LHS: Numerator = $(\cot A + \text{cosec } A) – 1$ Numerator = $(\cot A + \text{cosec } A) – (\text{cosec}^2 A - \cot^2 A)$ Numerator = $(\cot A + \text{cosec } A) – (\text{cosec } A - \cot A)(\text{cosec } A + \cot A)$ Now, factor out the common term $(\cot A + \text{cosec } A)$ from the numerator: Numerator = $(\cot A + \text{cosec } A) [1 – (\text{cosec } A - \cot A)]$ Numerator = $(\cot A + \text{cosec } A) [1 – \text{cosec } A + \cot A]$ Numerator = $(\cot A + \text{cosec } A) [\cot A – \text{cosec } A + 1]$ Substitute this back into the LHS expression: LHS = $\frac{(\cot A + \text{cosec } A) (\cot A – \text{cosec } A + 1)}{\cot A – \text{cosec } A + 1}$ Assume $\cot A – \text{cosec } A + 1 \neq 0$. Cancel the common factor from the numerator and the denominator: LHS = $\cot A + \text{cosec } A$ Rearrange the terms: LHS = $\text{cosec } A + \cot A$ This is equal to the Right Hand Side (RHS). LHS = RHS Hence Proved. (vi) Prove that $\sqrt{\frac{1 + \sin A}{1 - \sin A}} = \sec A + \tan A$: Consider the Left Hand Side (LHS): LHS = $\sqrt{\frac{1 + \sin A}{1 - \sin A}}$ Rationalize the denominator inside the square root by multiplying the numerator and denominator by the conjugate of the denominator, which is $1 + \sin A$: LHS = $\sqrt{\frac{(1 + \sin A)(1 + \sin A)}{(1 - \sin A)(1 + \sin A)}}$ LHS = $\sqrt{\frac{(1 + \sin A)^2}{1^2 - \sin^2 A}}$ Use the identity $1 - \sin^2 A = \cos^2 A$ in the denominator: LHS = $\sqrt{\frac{(1 + \sin A)^2}{\cos^2 A}}$ Take the square root of the numerator and the denominator: LHS = $\frac{\sqrt{(1 + \sin A)^2}}{\sqrt{\cos^2 A}}$ LHS = $\frac{|1 + \sin A|}{|\cos A|}$ For acute angle A ($0^\circ \leq A < 90^\circ$), $\sin A \geq 0$ and $\cos A \geq 0$. Thus $1 + \sin A$ is positive and $\cos A$ is positive. LHS = $\frac{1 + \sin A}{\cos A}$ Split the fraction into two terms: LHS = $\frac{1}{\cos A} + \frac{\sin A}{\cos A}$ Use the identities $\sec A = \frac{1}{\cos A}$ and $\tan A = \frac{\sin A}{\cos A}$: LHS = $\sec A + \tan A$ This is equal to the Right Hand Side (RHS). LHS = RHS Hence Proved. (vii) Prove that $\frac{\sin \theta – 2\sin^3 \theta}{2 \cos^3 \theta – \cos \theta} = \tan \theta$: Consider the Left Hand Side (LHS): LHS = $\frac{\sin \theta – 2\sin^3 \theta}{2 \cos^3 \theta – \cos \theta}$ Factor out $\sin \theta$ from the numerator and $\cos \theta$ from the denominator: LHS = $\frac{\sin \theta (1 – 2\sin^2 \theta)}{\cos \theta (2 \cos^2 \theta – 1)}$ We know that $\frac{\sin \theta}{\cos \theta} = \tan \theta$. So, the expression is $\tan \theta \times \frac{1 – 2\sin^2 \theta}{2 \cos^2 \theta – 1}$. Now we need to show that $\frac{1 – 2\sin^2 \theta}{2 \cos^2 \theta – 1} = 1$. Use the identity $\sin^2 \theta + \cos^2 \theta = 1$ to express the numerator or the denominator in terms of a single trigonometric function. Let's express the numerator in terms of $\cos \theta$ by using $\sin^2 \theta = 1 - \cos^2 \theta$: Numerator of the fraction = $1 – 2\sin^2 \theta = 1 – 2(1 - \cos^2 \theta)$ $= 1 – 2 + 2\cos^2 \theta = 2\cos^2 \theta - 1$ Substitute this back into the fraction part of the LHS: Fraction part = $\frac{2\cos^2 \theta - 1}{2 \cos^2 \theta – 1}$ Assuming $2 \cos^2 \theta - 1 \neq 0$, we can cancel the terms: Fraction part = 1 So, LHS = $\tan \theta \times 1$ LHS = $\tan \theta$ This is equal to the Right Hand Side (RHS). LHS = RHS Hence Proved. (viii) Prove that $(\sin A + \text{cosec } A)^2 + (\cos A + \sec A)^2 = 7 + \tan^2 A + \cot^2 A$: Consider the Left Hand Side (LHS): LHS = $(\sin A + \text{cosec } A)^2 + (\cos A + \sec A)^2$}
Expand the squares using $(a+b)^2 = a^2 + 2ab + b^2$: $(\sin A + \text{cosec } A)^2 = \sin^2 A + 2 \sin A \text{ cosec } A + \text{cosec}^2 A$ $(\cos A + \sec A)^2 = \cos^2 A + 2 \cos A \sec A + \sec^2 A$ Substitute these expanded forms back into the LHS: LHS = $(\sin^2 A + 2 \sin A \text{ cosec } A + \text{cosec}^2 A) + (\cos^2 A + 2 \cos A \sec A + \sec^2 A)$ Rearrange the terms: LHS = $\sin^2 A + \cos^2 A + 2 \sin A \text{ cosec } A + 2 \cos A \sec A + \text{cosec}^2 A + \sec^2 A$ Use the identities $\sin^2 A + \cos^2 A = 1$, $\sin A \text{ cosec } A = \sin A \times \frac{1}{\sin A} = 1$, and $\cos A \sec A = \cos A \times \frac{1}{\cos A} = 1$: LHS = $1 + 2(1) + 2(1) + \text{cosec}^2 A + \sec^2 A$ LHS = $1 + 2 + 2 + \text{cosec}^2 A + \sec^2 A$ LHS = $5 + \text{cosec}^2 A + \sec^2 A$}
We need the RHS in terms of $\tan^2 A$ and $\cot^2 A$. Use the identities $\text{cosec}^2 A = 1 + \cot^2 A$ and $\sec^2 A = 1 + \tan^2 A$: LHS = $5 + (1 + \cot^2 A) + (1 + \tan^2 A)$ LHS = $5 + 1 + \cot^2 A + 1 + \tan^2 A$ LHS = $7 + \tan^2 A + \cot^2 A$ This is equal to the Right Hand Side (RHS). LHS = RHS Hence Proved. (ix) Prove that $(\text{cosec } A – \sin A)(\sec A – \cos A) = \frac{1}{\tan A + \cot A}$: As hinted, simplify LHS and RHS separately. Consider the Left Hand Side (LHS): LHS = $(\text{cosec } A – \sin A)(\sec A – \cos A)$ Express $\text{cosec } A$ and $\sec A$ in terms of $\sin A$ and $\cos A$: $\text{cosec } A = \frac{1}{\sin A}$ and $\sec A = \frac{1}{\cos A}$. Substitute these into the LHS: LHS = $\left(\frac{1}{\sin A} – \sin A\right)\left(\frac{1}{\cos A} – \cos A\right)$ Find a common denominator within each parenthesis: $\frac{1}{\sin A} – \sin A = \frac{1}{\sin A} – \frac{\sin^2 A}{\sin A} = \frac{1 - \sin^2 A}{\sin A}$ $\frac{1}{\cos A} – \cos A = \frac{1}{\cos A} – \frac{\cos^2 A}{\cos A} = \frac{1 - \cos^2 A}{\cos A}$ Use the identities $1 - \sin^2 A = \cos^2 A$ and $1 - \cos^2 A = \sin^2 A$: Substitute these back into the LHS expression: LHS = $\left(\frac{\cos^2 A}{\sin A}\right)\left(\frac{\sin^2 A}{\cos A}\right)$ Multiply the two fractions: LHS = $\frac{\cos^2 A \sin^2 A}{\sin A \cos A}$ Assume $\sin A \neq 0$ and $\cos A \neq 0$. Cancel common terms: LHS = $\frac{(\cos A \cancel{\cos A}) (\sin A \cancel{\sin A})}{\cancel{\sin A} \cancel{\cos A}}$ LHS = $\cos A \sin A$ Now, consider the Right Hand Side (RHS): RHS = $\frac{1}{\tan A + \cot A}$ Express $\tan A$ and $\cot A$ in terms of $\sin A$ and $\cos A$: $\tan A = \frac{\sin A}{\cos A}$ and $\cot A = \frac{\cos A}{\sin A}$. Substitute these into the denominator of the RHS: RHS = $\frac{1}{\frac{\sin A}{\cos A} + \frac{\cos A}{\sin A}}$ Find a common denominator in the denominator of the main fraction. The common denominator is $\sin A \cos A$. $\frac{\sin A}{\cos A} + \frac{\cos A}{\sin A} = \frac{\sin A \times \sin A}{\cos A \times \sin A} + \frac{\cos A \times \cos A}{\sin A \times \cos A} = \frac{\sin^2 A + \cos^2 A}{\sin A \cos A}$ Use the identity $\sin^2 A + \cos^2 A = 1$ in the numerator: = $\frac{1}{\sin A \cos A}$ Substitute this back into the RHS expression: RHS = $\frac{1}{\frac{1}{\sin A \cos A}}$ Invert the denominator and multiply: RHS = $1 \times (\sin A \cos A)$ RHS = $\sin A \cos A$ Since LHS = $\cos A \sin A$ and RHS = $\sin A \cos A$, we have: LHS = RHS Hence Proved. (x) Prove that $\left( \frac{1 + \tan^2 A}{1 + \cot^2 A} \right) = \left(\frac{1 - \tan A}{1 - \cot A} \right)^{2} = \tan^2 A$: This identity has two parts to prove: Part 1: $\frac{1 + \tan^2 A}{1 + \cot^2 A} = \tan^2 A$ Part 2: $\left(\frac{1 - \tan A}{1 - \cot A} \right)^{2} = \tan^2 A$ If both parts are shown to be equal to $\tan^2 A$, then all three parts are equal to each other. Part 1: Prove $\frac{1 + \tan^2 A}{1 + \cot^2 A} = \tan^2 A$: Consider the Left Hand Side (LHS): LHS = $\frac{1 + \tan^2 A}{1 + \cot^2 A}$ Use the identities $\sec^2 A = 1 + \tan^2 A$ and $\text{cosec}^2 A = 1 + \cot^2 A$. Substitute these into the LHS: LHS = $\frac{\sec^2 A}{\text{cosec}^2 A}$ Express $\sec^2 A$ and $\text{cosec}^2 A$ in terms of $\sin A$ and $\cos A$: $\sec^2 A = \frac{1}{\cos^2 A}$ and $\text{cosec}^2 A = \frac{1}{\sin^2 A}$. Substitute these into the LHS: LHS = $\frac{\frac{1}{\cos^2 A}}{\frac{1}{\sin^2 A}}$ Invert the denominator and multiply: LHS = $\frac{1}{\cos^2 A} \times \frac{\sin^2 A}{1} = \frac{\sin^2 A}{\cos^2 A}$ Using the identity $\frac{\sin A}{\cos A} = \tan A$, we have $\frac{\sin^2 A}{\cos^2 A} = \tan^2 A$. LHS = $\tan^2 A$ This is equal to the Right Hand Side (RHS) of the first part. Part 1 is Proved. Part 2: Prove $\left(\frac{1 - \tan A}{1 - \cot A} \right)^{2} = \tan^2 A$: Consider the Left Hand Side (LHS): LHS = $\left(\frac{1 - \tan A}{1 - \cot A} \right)^{2}$ Express $\cot A$ in terms of $\tan A$ using the identity $\cot A = \frac{1}{\tan A}$. Substitute this into the denominator of the fraction inside the square: LHS = $\left(\frac{1 - \tan A}{1 - \frac{1}{\tan A}} \right)^{2}$ Simplify the denominator of the inner fraction by finding a common denominator: $1 - \frac{1}{\tan A} = \frac{\tan A - 1}{\tan A}$ Substitute this back into the LHS expression: LHS = $\left(\frac{1 - \tan A}{\frac{\tan A - 1}{\tan A}} \right)^{2}$ Invert the denominator of the main fraction and multiply: LHS = $\left((1 - \tan A) \times \frac{\tan A}{\tan A - 1} \right)^{2}$ Notice that $(1 - \tan A) = - (\tan A - 1)$. Substitute this into the expression: LHS = $\left(- (\tan A - 1) \times \frac{\tan A}{\tan A - 1} \right)^{2}$}
Assume $\tan A - 1 \neq 0$ (i.e., $\tan A \neq 1$, $A \neq 45^\circ$, etc.). Cancel the common factor $(\tan A - 1)$:
LHS = $(- \tan A)^2$ LHS = $(-\tan A) \times (-\tan A) = \tan^2 A$ This is equal to the Right Hand Side (RHS) of the second part. Part 2 is Proved. Since both parts are equal to $\tan^2 A$, the given identity is true. Hence Proved.

